4.1.1 Hyperbolic Functions & Graphs

Understanding Hyperbolic Functions

Hyperbolic functions are analogues of trigonometric functions, but they are defined using exponential functions. The three primary hyperbolic functions are:

Hyperbolic Sine ($\sinh x$)

$$\sinh x = \frac{e^x - e^{-x}}{2}$$

Domain:

($-\infty, \infty$)

Range:

($-\infty, \infty$)

Hyperbolic Cosine ($\cosh x$)

$$\cosh x = \frac{e^x + e^{-x}}{2}$$

Domain:

$(-\infty, \infty)$

Range:

$[1, \infty)$

Hyperbolic Tangent ($\tanh x$)

$$\tanh x = \frac{\sinh x}{\cosh x} = \frac{e^x - e^{-x}}{e^x + e^{-x}}$$

Domain:

$(-\infty, \infty)$

Range:

$(-1, 1)$

Graphs of Hyperbolic Functions

Graph of $\sinh x$

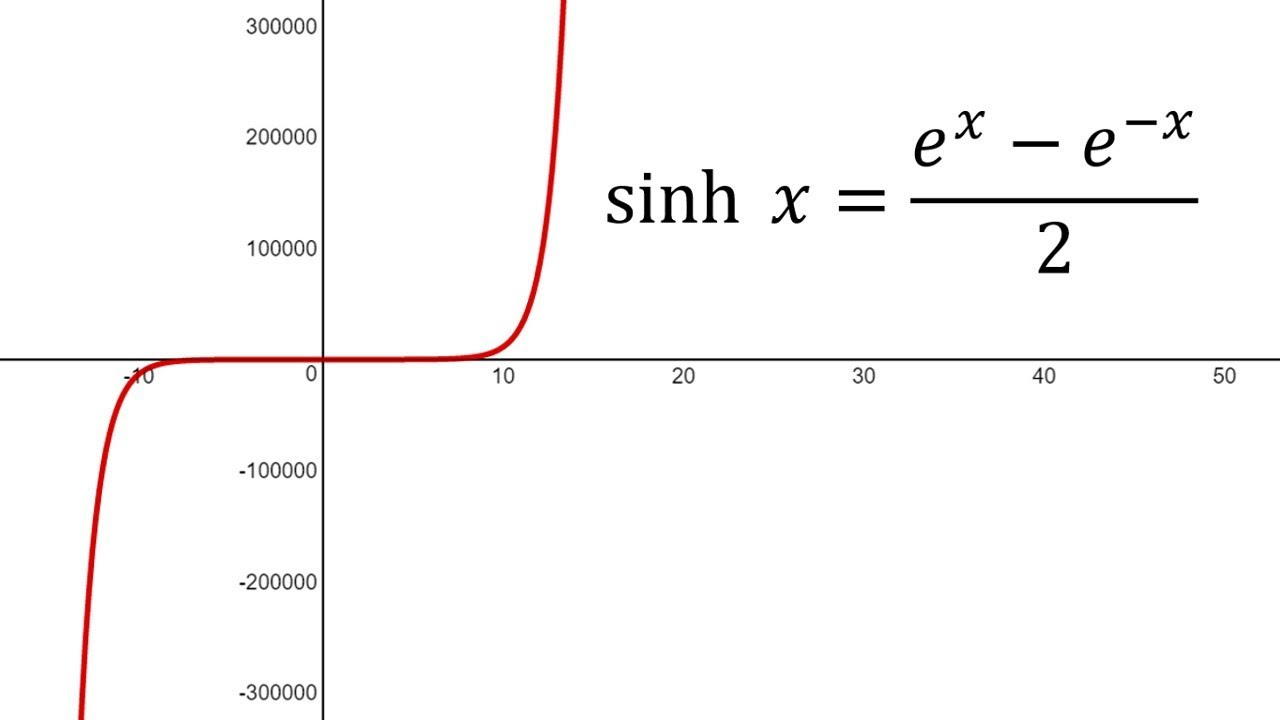
• Shape: Odd function (symmetric about the origin).
• Crosses the origin $(0, 0)$
• Rapidly increases as $x \to \infty$ and decreases as $x \to -\infty$

Graph of $\cosh x$

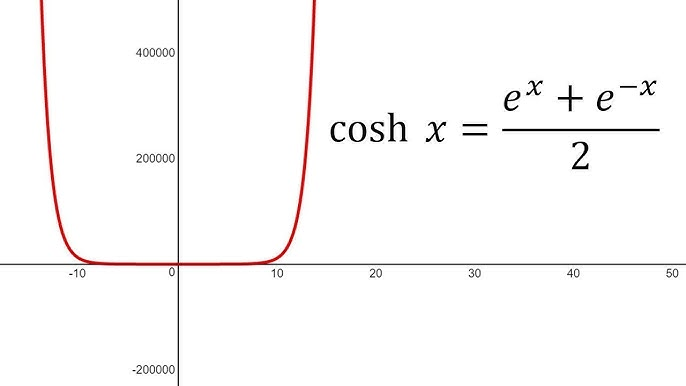
• Shape: Even function (symmetric about the $y-axis$).
• Always above or equal to $1$.

Graph of $\tanh x$

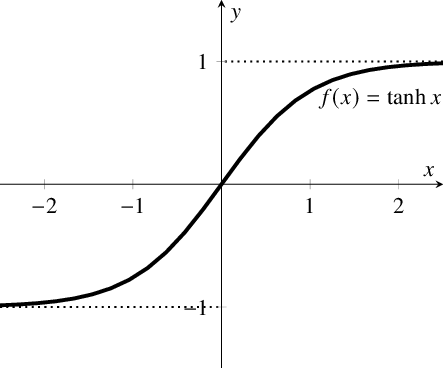
• Shape: Odd function (symmetric about the origin).
• Asymptotes: $y=-1$ and $y=1$
• Passes through the origin ($0, 0$).

Worked Example

Note Summary