Photo AI
a) Factorise fully 9a² - 6ab + 12ac - 8bc - Junior Cycle Mathematics - Question Question 1 - 2014
Question Question 1
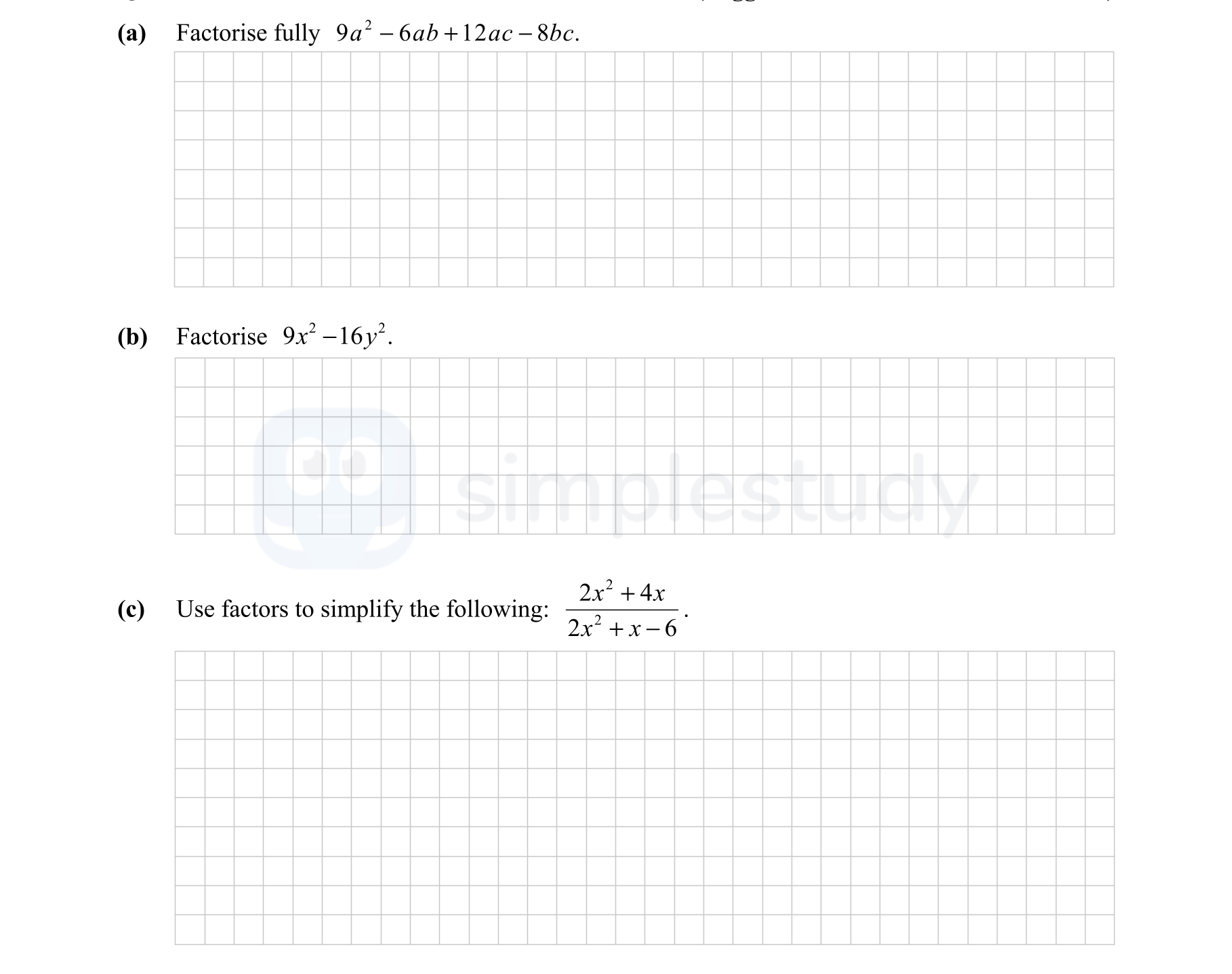
a) Factorise fully 9a² - 6ab + 12ac - 8bc. b) Factorise 9x² - 16y². c) Use factors to simplify the following: \( \frac{2x² + 4x}{2x² + x - 6} \).
Worked Solution & Example Answer:a) Factorise fully 9a² - 6ab + 12ac - 8bc - Junior Cycle Mathematics - Question Question 1 - 2014
Step 1
Factorise fully 9a² - 6ab + 12ac - 8bc.
Answer
To factorise the expression, we look for common factors:
- Group the terms: 9a² - 6ab + 12ac - 8bc = (9a² - 6ab) + (12ac - 8bc).
- Factor out the common factors in each group:
- From the first group (9a² - 6ab), factor out 3a: [ 3a(3a - 2b) ]
- From the second group (12ac - 8bc), factor out 4c: [ 4c(3a - 2b) ]
- Now, we can combine these two factored terms: [ 3a(3a - 2b) + 4c(3a - 2b) = (3a + 4c)(3a - 2b) ]
Step 2
Factorise 9x² - 16y².
Answer
This expression represents a difference of squares, which can be factored using the formula ( a² - b² = (a - b)(a + b) ).
- Identify a and b:
- Here, ( a = 3x ) and ( b = 4y ), so we have: [ 9x² - 16y² = (3x)² - (4y)² ]
- Applying the difference of squares formula: [ 9x² - 16y² = (3x - 4y)(3x + 4y) ]
Step 3
Use factors to simplify the following: 2x² + 4x / 2x² + x - 6.
Answer
To simplify the expression ( \frac{2x² + 4x}{2x² + x - 6} ), we will factor both the numerator and the denominator:
- Factor the numerator: [ 2x² + 4x = 2x(x + 2) ]
- Factor the denominator:
- To factor ( 2x² + x - 6 ), we can use the factorization method:
- Find two numbers that multiply to ( 2 \times -6 = -12 ) and add to ( 1 ) (which is the coefficient of x): these numbers are ( 4 ) and ( -3 ).
- Thus: [ 2x² + x - 6 = 2x² + 4x - 3x - 6 = 2x(x + 2) - 3(x + 2) = (2x - 3)(x + 2) ]
- Substitute back into the expression: [ \frac{2x(x + 2)}{(2x - 3)(x + 2)} ]
- Cancel out the common factor (x + 2): [ \frac{2x}{2x - 3} ]
Thus, the simplified form is ( \frac{2x}{2x - 3} ).
