In the right-angled triangle shown in the diagram, one of the acute angles is four times as large as the other acute angle. (i) Find the measures of the two acute angles in the triangle. (ii) The triangle in part (i) is placed on a co-ordinate diagram. The base is parallel to the x-axis. Find the slope of the line l that contains the hypotenuse of the triangle. Give your answer correct to three decimal places.

Junior Cycle Mathematics Co-Ordinate Geometry: In the right-angled triangle sho

In the right-angled triangle shown in the diagram, one of the acute angles is four times as large as the other acute angle - Junior Cycle Mathematics - Question 17 - 2014

Question 17

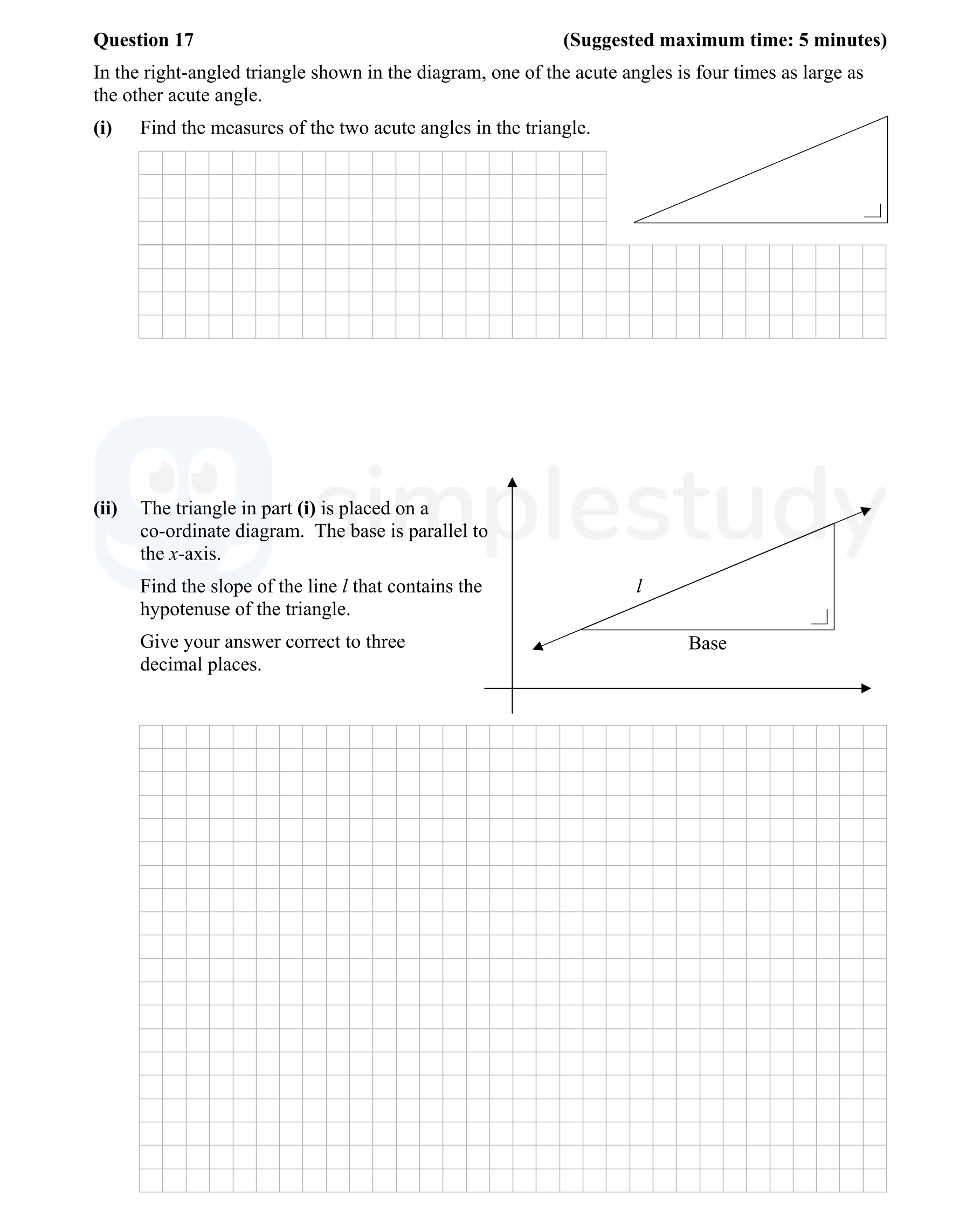
In-the-right-angled-triangle-shown-in-the-diagram,-one-of-the-acute-angles-is-four-times-as-large-as-the-other-acute-angle-Junior Cycle Mathematics-Question 17-2014.png

In the right-angled triangle shown in the diagram, one of the acute angles is four times as large as the other acute angle. (i) Find the measures of the two acute a... show full transcript

Worked Solution & Example Answer:In the right-angled triangle shown in the diagram, one of the acute angles is four times as large as the other acute angle - Junior Cycle Mathematics - Question 17 - 2014

Step 1

Find the measures of the two acute angles in the triangle.

96%

114 rated

Answer

Let the smallest acute angle be denoted as $x$ . Then, the other acute angle is $4x$ . Since the sum of the angles in a triangle is $180^{ ext{o}}$ and accounting for the right angle, we can set up the equation:

$x + 4x + 90^{ ext{o}} = 180^{ ext{o}}$

Combining like terms gives:

$5x + 90^{ ext{o}} = 180^{ ext{o}}$

Subtracting $90^{ ext{o}}$ from both sides yields:

$5x = 90^{ ext{o}}$

Dividing both sides by 5 gives:

$x = 18^{ ext{o}}$

Thus, the two acute angles are:

The smallest angle: $x = 18^{ ext{o}}$
The larger angle: $4x = 72^{ ext{o}}$

Step 2

Find the slope of the line l that contains the hypotenuse of the triangle.

99%

104 rated

Answer

The slope of a line can be calculated as the change in y-values divided by the change in x-values. In this triangle, the hypotenuse creates an angle of $18^{ ext{o}}$ with the base parallel to the x-axis, where we know:

$\text{slope} = \tan(\theta)$

Substituting the angle we found, we have:

$\text{slope} = \tan(18^{\text{o}})$

Using a calculator, we find:

$\tan(18^{\text{o}}) \approx 0.325$

Therefore, the slope of line l is $0.325$ correct to three decimal places.

In the right-angled triangle shown in the diagram, one of the acute angles is four times as large as the other acute angle - Junior Cycle Mathematics - Question 17 - 2014

Worked Solution & Example Answer:In the right-angled triangle shown in the diagram, one of the acute angles is four times as large as the other acute angle - Junior Cycle Mathematics - Question 17 - 2014

Find the measures of the two acute angles in the triangle.

Find the slope of the line l that contains the hypotenuse of the triangle.

Join the Junior Cycle students using SimpleStudy...