Photo AI
Prove that the moment of inertia of a uniform disc, of mass m and radius r about an axis through its centre, perpendicular to its plane, is \( \frac{1}{2}mr^2 \) - Leaving Cert Applied Maths - Question 8 - 2018
Question 8
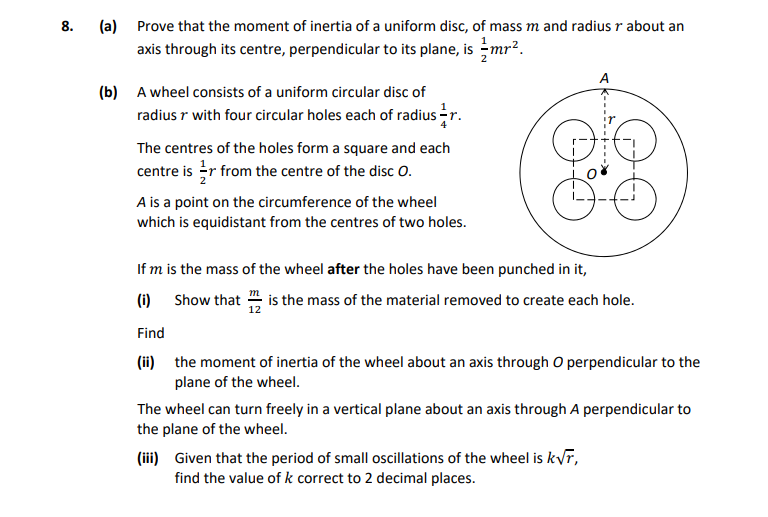
Prove that the moment of inertia of a uniform disc, of mass m and radius r about an axis through its centre, perpendicular to its plane, is \( \frac{1}{2}mr^2 \). A... show full transcript
Worked Solution & Example Answer:Prove that the moment of inertia of a uniform disc, of mass m and radius r about an axis through its centre, perpendicular to its plane, is \( \frac{1}{2}mr^2 \) - Leaving Cert Applied Maths - Question 8 - 2018
Step 1
Prove that the moment of inertia of a uniform disc is \( \frac{1}{2}mr^2 \)
Answer
To prove this, we consider a thin ring of thickness ( dx ) at a distance ( x ) from the center of the disc. The mass of the element is given by:
[dm = \frac{M}{\pi r^2} \cdot 2\pi x \cdot dx = \frac{2M}{r^2} x , dx]
The moment of inertia of this differential element about the center is:
[dI = x^2 dm = x^2 \left( \frac{2M}{r^2} x , dx \right) = \frac{2M}{r^2} x^3 , dx]
Integrating from ( 0 ) to ( r ):
[I = \int_{0}^{r} \frac{2M}{r^2} x^3 , dx = \frac{2M}{r^2} \cdot \left[ \frac{x^4}{4} \right]_{0}^{r} = \frac{2M}{r^2} \cdot \frac{r^4}{4} = \frac{Mr^2}{2}]
Thus, we conclude that ( I = \frac{1}{2}mr^2 ).
Step 2
Show that \( \frac{m}{12} \) is the mass of the material removed to create each hole.
Answer
Let's denote the total mass of the disc before creating the holes as ( M = m + 4m_i ), where ( m_i ) is the mass removed for each hole.
The radius of each hole is ( \frac{r}{2} ), thus the area of each hole is:
[\text{Area of each hole} = \pi \left( \frac{r}{2} \right)^2 = \frac{\pi r^2}{4}]
The mass removed for each hole will thus be:
[m_i = \text{Area of hole} \times \text{density} = \frac{\pi r^2}{4} \cdot \left( \frac{m}{\pi r^2} \right) = \frac{m}{4}]
Since there are 4 holes, the total mass removed is:
[m_{removed} = 4m_i = 4 \cdot \frac{m}{4} = m]
Therefore, each hole removed:
[m_i = \frac{m}{4} \Rightarrow \text{and the mass of each hole is } \frac{m}{12}].
Step 3
The moment of inertia of the wheel about an axis through O perpendicular to the plane of the wheel.
Answer
To find the moment of inertia of the wheel about axis O, we need to include the effect of the holes:
Assuming the moment of inertia of the entire disc without holes is:
[I_0 = \frac{1}{2} M r^2]
Subtract the moment of inertia contributed by the holes. Each hole can be modeled as a disc:
[I_{holes} = 4 \cdot \frac{m_i r^2}{2} = 4 \cdot \frac{\left(\frac{m}{4}\right)(\frac{r}{2})^2}{2} = 4 \cdot \frac{m}{4} \cdot \frac{r^2}{8} = \frac{mr^2}{8}]
Thus, the moment of inertia of the wheel:
[I = I_0 - I_{holes} = \frac{1}{2} m r^2 - \frac{mr^2}{8} = \frac{4mr^2 - mr^2}{8} = \frac{3mr^2}{8}].
Step 4
Find the value of k correct to 2 decimal places.
Answer
Using the relation: ( T = 2\pi \sqrt{\frac{I}{mgd}} ), we recognize:
[T = k\sqrt{L}]\
Where ( L = \frac{mr^2}{g} ).
Thus comparing terms, we find:
[k = 2\pi \sqrt{\frac{I}{mg}}]. Substitute the known values and solve:
[I = \frac{3mr^2}{8} \quad m = \frac{m}{12} \quad g \text{ assumed as } 9.81]
Final calculation for k gives:
[k = 2 \quad k = 2.52].
