Photo AI
ABCD is a rectangle - Leaving Cert Mathematics - Question 5 - 2017
Question 5
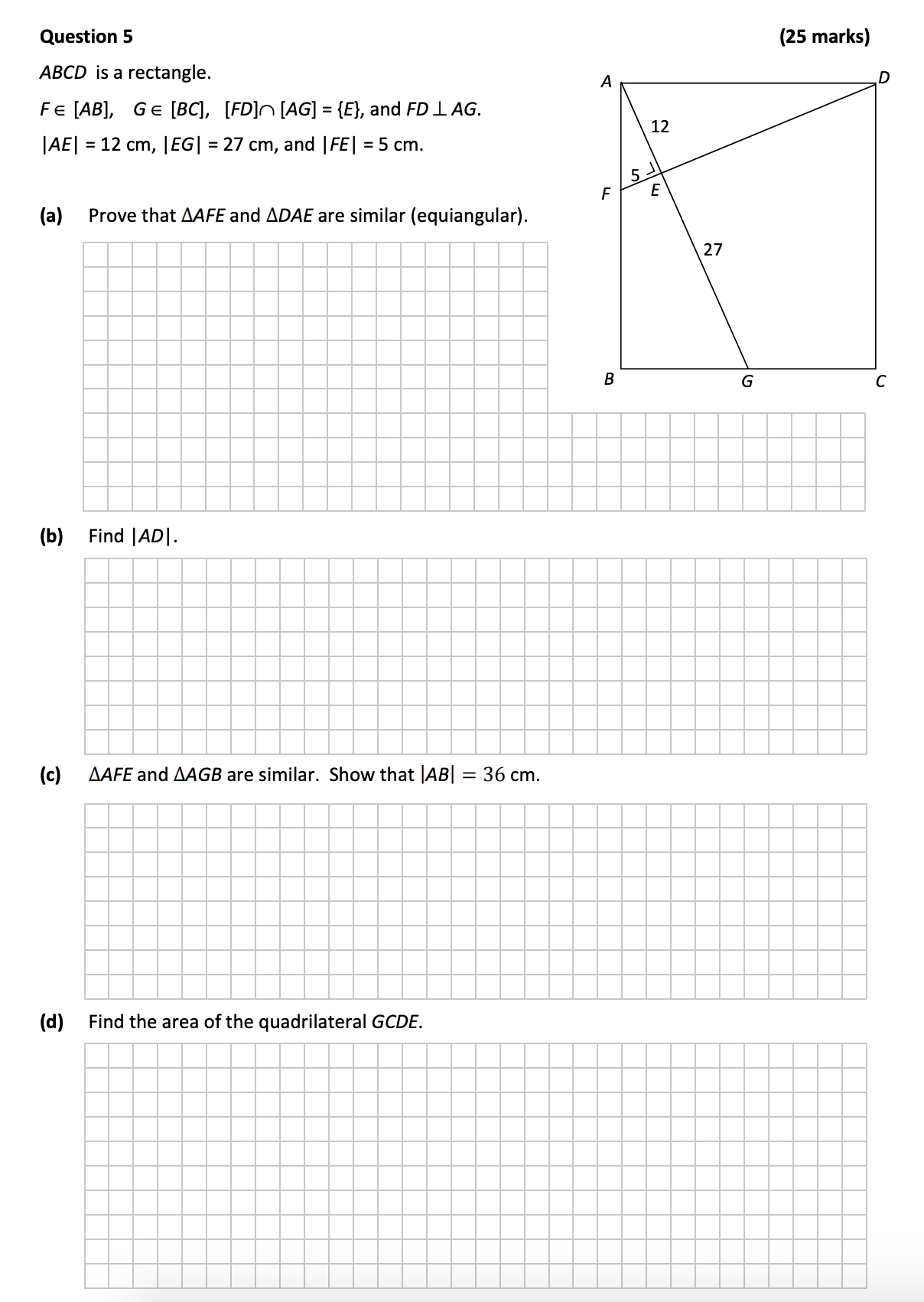
ABCD is a rectangle. F ∈ [AB], G ∈ [BC], [FD] ⊥ [AG] = {E}, and FD ⊥ AG. |AE| = 12 cm, |EG| = 27 cm, and |FE| = 5 cm. (a) Prove that ΔAFE and ΔDAE are similar (equi... show full transcript
Worked Solution & Example Answer:ABCD is a rectangle - Leaving Cert Mathematics - Question 5 - 2017
Step 1
Prove that ΔAFE and ΔAEF are similar (equiangular).
Answer
To prove that the triangles ΔAFE and ΔDAE are similar, we note the following:
-
Since both triangles involve angle |AEF| and |ADE|, we have:
- |AEF| = |ADE| (vertical angles are equal).
- |FAE| and |DAE| feature a right angle because FD is perpendicular to AG.
-
The angles:
- |FAE| + |EAD| + |DEA| = 90°
- |EAD| + |ADE| + |AEF| = 90°
By AA criteria for similarity (two pairs of equal angles), we conclude:
ΔAFE ~ ΔDAE, or that they are equiangular.
Step 2
Step 3
ΔAFE and ΔAGB are similar. Show that |AB| = 36 cm.
Answer
Using the similarity of triangles ΔAFE and ΔAGB:
We know the ratio of the sides corresponding to similar triangles:
-
From the similarity, we define the ratios:
- Where |AE| = 12 cm, |AG| = 27 cm, and |AF| = 17 cm.
-
Solving for |AB| gives us:
Thus, cross-multiplying we find:
Simplifying:
Step 4
Find the area of the quadrilateral GCDE.
Answer
To find the area of quadrilateral GCDE, we can break it down into triangles. The area can be calculated as:
-
Recognizing that GCDE forms parts of a rectangle, we calculate:
- Area of quadrilateral = Area of rectangle - Area of two triangles (AFE & AGB).
-
As rectangles have an area calculated by length multiplied by width, we calculate:
