Photo AI
In an experiment to measure the focal length of a converging lens, a student measured the image distance v for each of four different values of the object distance u - Leaving Cert Physics - Question 2 - 2012
Question 2
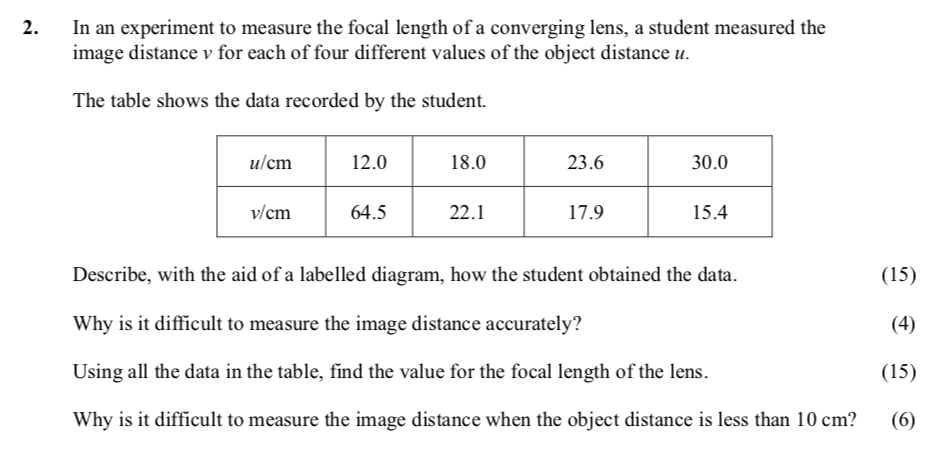
In an experiment to measure the focal length of a converging lens, a student measured the image distance v for each of four different values of the object distance u... show full transcript
Worked Solution & Example Answer:In an experiment to measure the focal length of a converging lens, a student measured the image distance v for each of four different values of the object distance u - Leaving Cert Physics - Question 2 - 2012
Step 1
Describe, with the aid of a labelled diagram, how the student obtained the data.
Answer
To measure the focal length of the converging lens, the student set up the apparatus as follows:
-
Apparatus Arrangement: The student used a convex lens mounted on a stand, a screen to capture the image, and a ruler to measure distances. The light source was positioned so that the light passed through the lens and projected an image on the screen.
-
Adjustment: The student adjusted the position of the screen until a sharp image was formed. This adjustment was crucial as it ensured that the image was clear enough to obtain accurate measurements.
-
Measurements: For various object distances (u), the corresponding image distances (v) were recorded. The student carefully measured and noted these distances in the table provided.
-
Repeating the Experiment: The student repeated the above steps for each of the four specified object distances, ensuring accuracy in each measurement and recording the data methodically.
Step 2
Why is it difficult to measure the image distance accurately?
Answer
Measuring the image distance accurately can be challenging due to several factors:
-
Parallax Error: When reading measurements, parallax can cause significant errors if the observer does not align their line of sight directly with the measurement scale.
-
Focus Adjustment: If the image is not perfectly sharp, it can be difficult to determine the exact point where the image is formed, leading to inaccuracies in the measured distance.
-
Lens Aberration: Converging lenses can exhibit optical aberrations, particularly when the light rays are not parallel to the optical axis, which can cause distortion in the image and complicate the measurement.
Step 3
Using all the data in the table, find the value for the focal length of the lens.
Answer
To find the focal length of the lens, we can use the lens formula:
-
For each pair of measured values of u and v, compute ( \frac{1}{u} ) and ( \frac{1}{v} ):
- For u = 12.0 cm, v = 64.5 cm: ( \frac{1}{u} = 0.0833 ), ( \frac{1}{v} = 0.0155 )
- For u = 18.0 cm, v = 22.1 cm: ( \frac{1}{u} = 0.0556 ), ( \frac{1}{v} = 0.0452 )
- For u = 23.6 cm, v = 17.9 cm: ( \frac{1}{u} = 0.0424 ), ( \frac{1}{v} = 0.0558 )
- For u = 30.0 cm, v = 15.4 cm: ( \frac{1}{u} = 0.0333 ), ( \frac{1}{v} = 0.0650 )
-
Next, apply the lens formula to calculate f for each set of data:
- For (u = 12.0 cm, v = 64.5 cm): ( f = \frac{uv}{u+v} \approx 10.12 , cm )
- For (u = 18.0 cm, v = 22.1 cm): ( f \approx 9.21 , cm )
- For (u = 23.6 cm, v = 17.9 cm): ( f \approx 10.48 , cm )
- For (u = 30.0 cm, v = 15.4 cm): ( f \approx 10.18 , cm )
-
Average the focal lengths calculated: ( f_{average} = \frac{10.12 + 9.21 + 10.48 + 10.18}{4} \approx 10.10 , cm )
Thus, the focal length of the lens is approximately 10.10 cm.
Step 4
Why is it difficult to measure the image distance when the object distance is less than 10 cm?
Answer
Measuring the image distance when the object distance is less than 10 cm presents particular challenges:
-
Virtual Images: At short object distances, the lens may produce a virtual image where the image forms on the same side as the object. These images cannot be projected onto a screen, complicating measurement.
-
Sharpness: As the object distance decreases, achieving a sharp focus can become more difficult. This can lead to uncertainties in locating the true position of the image and hence errors in measurement.
-
Limited Measurement Scope: The shorter the distance, the less room there is for adjusting the screen for accurate measurement, increasing the likelihood of errors.
