Area and Volume Formulae

Understanding how to calculate the area and volume of various shapes is crucial for solving problems in geometry. These concepts are fundamental in Junior Cycle Maths and are often tested in exams. Let's break down the essential formulas, what each variable represents, and include some exam tips to help you succeed.

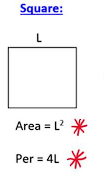
1. Square

Area $(A)$ $(A)$ : $\text{A} = L^2$ $A = L^{2}$ The area of a square is found by multiplying the length of one side by itself.
- $L$ : Length of one side of the square.
Perimeter $(P)$ : $\text{P} = 4L$ The perimeter is the total length around the square, which is four times the length of one side.

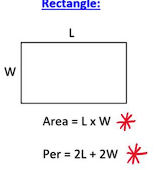
2. Rectangle

Area $(A)$ $(A)$ : $\text{A} = L \times W$ $A = L \times W$ The area of a rectangle is calculated by multiplying its length by its width.
- $L$ : Length of the rectangle.
- $W$ : Width of the rectangle.
Perimeter $(P)$ : $\text{P} = 2L + 2W$ The perimeter is the total distance around the rectangle, which is twice the length plus twice the width.

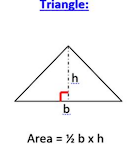
3. Triangle

Area $(A)$ $(A)$ : $\text{A} = \frac{1}{2} \times b \times h$ $A = \frac{1}{2} \times b \times h$ The area of a triangle is half the product of its base and height.
- $b$ : Base of the triangle.
- $h$ : Height of the triangle (the perpendicular distance from the base to the opposite vertex).

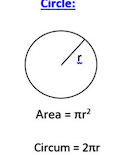
4. Circle

Area $(A)$ $(A)$ : $\text{A} = \pi r^2$ $A = π r^{2}$ The area of a circle is found by multiplying pi $(\pi \approx 3.14)$ by the square of the radius.
- $r$ : Radius of the circle (distance from the center to any point on the circle).
Circumference $(C)$ : $\text{C} = 2\pi r$ The circumference is the total distance around the circle, calculated by multiplying $2$ , $pi,$ and the $radius$ .

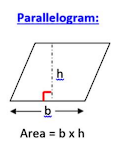
5. Parallelogram

Area $(A)$ $(A)$ : $\text{A} = b \times h$ $A = b \times h$ The area of a parallelogram is the product of its base and height.
- $b$ : Base of the parallelogram.
- $h$ : Height of the parallelogram (the perpendicular distance between the base and the opposite side).

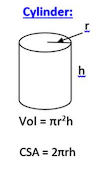
6. Cylinder

Volume $(V)$ $(V)$ : $\text{V} = \pi r^2 h$ $V = π r^{2} h$ The volume of a cylinder is found by multiplying the area of its circular base by its height.
- $r$ : Radius of the base of the cylinder.
- $h$ : Height of the cylinder.
Curved Surface Area $(CSA)$ : $\text{CSA} = 2\pi rh$ The curved surface area is the area around the side of the cylinder.

infoNote

Exam Tip: Understanding Surface Areas

Be careful when dealing with surface area calculations. $Curved$ $Surface$ $Area$ $(CSA)$ only includes the sides of shapes like cylinders and does not account for the top and bottom. In contrast, $Total$ $Surface$ $Area$ $(TSA)$ includes all the surfaces.

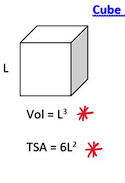
7. Cube

Volume $(V)$ $(V)$ : $\text{V} = L^3$ $V = L^{3}$ For a cube, the volume is the cube of the length of one side.
- $L$ : Length of one side of the cube.
Total Surface Area $(TSA)$ : $\text{TSA} = 6L^2$ The total surface area is six times the area of one face of the cube (since a cube has six faces).

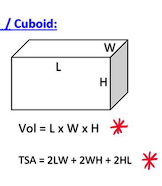
8. Cuboid

Volume $(V)$ $(V)$ : $\text{V} = L \times W \times H$ $V = L \times W \times H$ The volume of a cuboid is the product of its length, width, and height.
- $L$ : Length of the cuboid.
- $W$ : Width of the cuboid.
- $H$ : Height of the cuboid.
Total Surface Area $(TSA)$ : $\text{TSA} = 2LW + 2WH + 2HL$ The total surface area is the sum of the areas of all six faces of the cuboid.

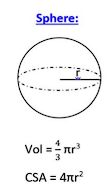
9. Sphere

Volume $(V)$ $(V)$ : $\text{V} = \frac{4}{3} \pi r^3$ $V = \frac{4}{3} π r^{3}$ The volume of a sphere is calculated using the formula above, where the radius is cubed.
- $r$ : Radius of the sphere.
Curved Surface Area $(CSA)$ : $\text{CSA} = 4\pi r^2$ The curved surface area is four times the area of a circle with the same radius as the sphere.

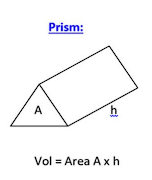
10. Prism

Volume $(V)$ $(V)$ : $\text{V} = \text{Area of base (A)} \times h$ $V = Area of base (A) \times h$ The volume of a prism is the product of the area of its base and its height.
- $A$ : Area of the base of the prism.
- $h$ : Height of the prism (the perpendicular distance between the two bases).