Photo AI
Last Updated Sep 26, 2025
Practice Problems Simplified Revision Notes for Junior Cycle Mathematics
Revision notes with simplified explanations to understand Practice Problems quickly and effectively.
228+ students studying
Practice Problems
Problems:
Problem 1: Evaluating a Function
Question: Given the function , find:
Explanation**:**
When you see a function like this, it's like a machine that takes an input number (in this case, ), does some calculations, and gives you an output. Here, you're asked to find out what happens when you put and into the machine.
Problem 2: Finding Inputs for a Function
Question: If , find the value of when .
Explanation**:**
Normally, you would put a number into a function and find the result. Here, you're given the result and need to figure out what number you started with (that is, ). To do this, you'll work backward, like solving a puzzle in reverse.
Problem 3: Graphing a Linear Function
Question: Graph the linear function for values from to .
Explanation**:**
To draw a picture of this function on a graph, you need to find out what is for different values of . After you have a few points, you can connect them to see the full picture, which will be a straight line.
Problem 4: Finding the Roots of a Quadratic Function
Question: Find the roots of the quadratic function .
Explanation**:**
The "roots" of a function are the points where the function touches the x-axis (where ). To find these points, we solve the equation by setting . You can find these points by factorizing the equation or using a special formula called the quadratic formula.
Problem 5: Solving a System of Linear Functions
Question: If and , find the value of where .
Explanation**:**
Here, we're asked to find out where two different functions give the same result for the same value of . This is like finding the spot where two lines cross each other on a graph. To do this, we set the two functions equal to each other and solve for .
Solutions:
Problem 1: Evaluating a Function
Question: Given the function , find:
For :
-
First, replace with in the function. This is like plugging into the machine to see what comes out.
-
Plug in :
-
Now, do the math:
-
Answer: . For :
-
Next, replace with and do the same thing.
-
Plug in :
-
Now, do the math:
-
Answer: . Explanation:
We replaced with the given numbers and followed the function's steps to see what comes out. This helps us understand how the function behaves for different inputs.
Problem 2: Finding Inputs for a Function
Question: If , find the value of when
To find when :
- Start by setting the function equal to because that's the result we're given. We need to figure out what number makes this happen.
- Set up the equation:
- First, add to both sides to undo the subtraction. This gets us closer to isolating :
- Next, divide by to find . We divide because is multiplied by , and dividing cancels this out:
- Answer: . Explanation:
We worked backward from the result to find the starting number . By undoing each operation step by step, we were able to solve for .
Problem 3: Graphing a Linear Function
Question: Graph the linear function for values from to .
Points to calculate:
-
We start by choosing different values for , and then we calculate the corresponding values. This helps us see where the function is on the graph.
-
Calculate for each value of :
- When :
- When :
- When :
- When :
- When :
-
Next, plot these points on a graph. For example, plot the point by going to on the x-axis and up to on the y-axis.
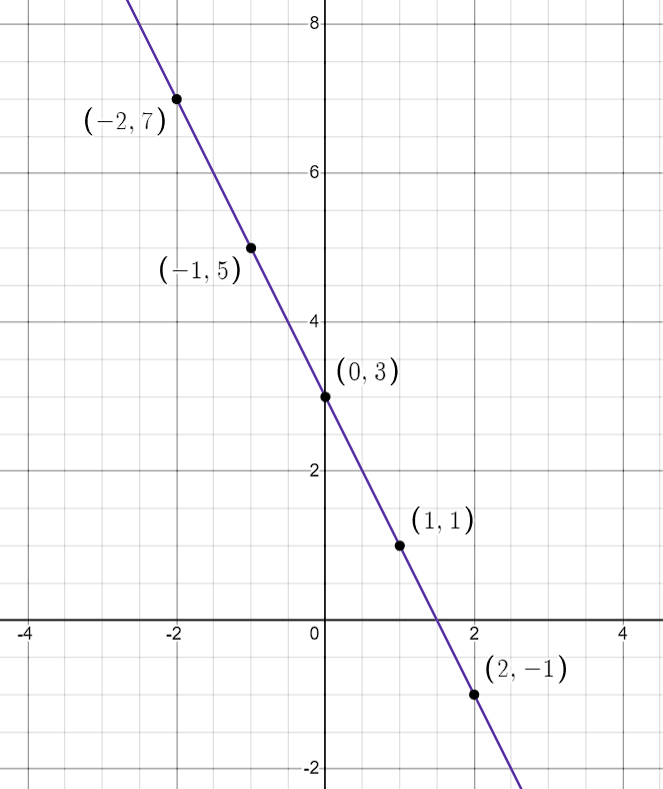
-
Finally, connect the dots with a straight line to complete the graph of the function. Explanation:
By calculating the values for different values, we can plot these points and connect them to draw the function. Since it's a linear function, the points will always line up in a straight line.
Problem 4: Finding the Roots of a Quadratic Function
Question: Find the roots of the quadratic function .
- The roots are the points where the function equals zero. So, we need to find out where .
- Set the equation:
- To find the roots, we factorise the quadratic equation, which is like breaking it down into two simpler pieces.
- Factorise:
- Now, solve for by setting each factor equal to zero:
- Answer: The roots are and . Explanation:
We found the roots by solving the equation where the function equals zero, which shows us where the graph crosses the x-axis. If factorizing is difficult, you can also use the quadratic formula to find the roots.
Problem 5: Solving a System of Linear Functions
Question: If and , find the value of where .
- We need to find the point where both functions give the same result. This is like finding where two lines cross on a graph.
- Start by setting the functions equal to each other:
- Next, move the terms to one side by subtracting from both sides:
- Finally, subtract from both sides to isolate :
- Answer: . Explanation:
We set the two functions equal to find where they give the same result. By solving for , we find the value where the two lines intersect. If you input into either function, they will both give the same output.
500K+ Students Use These Powerful Tools to Master Practice Problems For their Junior Cycle Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
50 flashcards
Flashcards on Practice Problems
Revise key concepts with interactive flashcards.
Try Mathematics Flashcards2 quizzes
Quizzes on Practice Problems
Test your knowledge with fun and engaging quizzes.
Try Mathematics Quizzes29 questions
Exam questions on Practice Problems
Boost your confidence with real exam questions.
Try Mathematics Questions27 exams created
Exam Builder on Practice Problems
Create custom exams across topics for better practice!
Try Mathematics exam builder80 papers
Past Papers on Practice Problems
Practice past papers to reinforce exam experience.
Try Mathematics Past PapersOther Revision Notes related to Practice Problems you should explore
Discover More Revision Notes Related to Practice Problems to Deepen Your Understanding and Improve Your Mastery
Load more notes