Sine, Cosine and Tangent

This section covers how to use Sine (Sin), Cosine (Cos), and Tangent (Tan) to solve problems in right-angled triangles. These tools help find missing sides or angles in right-angled triangles. The explanations are broken down step by step for clarity.

What Are Sine, Cosine, and Tangent?

Sine, Cosine, and Tangent are functions that relate the angles of a right-angled triangle to the lengths of its sides. Specifically, they compare certain sides of the triangle relative to a given angle, called Angle A.

Here's how each function works:

Sine of Angle A: Compares the length of the side opposite Angle A to the length of the hypotenuse. $\sin(A) = \frac{\text{Opposite}}{\text{Hypotenuse}}$
Cosine of Angle A: Compares the length of the side adjacent to Angle A to the length of the hypotenuse. $\cos(A) = \frac{\text{Adjacent}}{\text{Hypotenuse}}$
Tangent of Angle A: Compares the length of the side opposite Angle A to the length of the side adjacent to Angle A. $\tan(A) = \frac{\text{Opposite}}{\text{Adjacent}}$ These formulas help find either the length of a side or the size of an angle in a right-angled triangle.

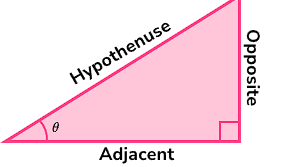
Step 1: Identify the Sides of the Triangle Relative to Angle A

Before using these formulas, it is necessary to determine which sides of the triangle are involved based on Angle A.

Opposite side: This is the side directly across from Angle A.
Adjacent side: This is the side next to Angle A (but not the hypotenuse).
Hypotenuse: This is always the longest side and is opposite the right angle.

Step 2: Choose the Right Ratio (Sine, Cosine, or Tangent)

Next, decide which ratio to use—Sine, Cosine, or Tangent—depending on what sides of the triangle are known and what needs to be found.

If the opposite and hypotenuse are known or one of them needs to be found, use Sine.
If the adjacent and hypotenuse are known or one of them needs to be found, use Cosine.
If the opposite and adjacent are known or one of them needs to be found, use Tangent.

infoNote

Example 1: Finding a Side Given an Angle and a Side (Using Sine)

Problem: In a right-angled triangle, Angle A is 30° and the hypotenuse is 10 cm. Find the length of the side opposite Angle A.

Step 1: Identify the sides.

Opposite side is x.
Hypotenuse is 10 cm.

Step 2: Choose the ratio. Since the opposite side and the hypotenuse are involved, and the opposite side needs to be found, use Sine:

$\sin(30°) = \frac{x}{10}$

Step 3: Solve for x. First, find the value of $\sin(30°)$ using a calculator (make sure it is in degrees mode):

$\sin(30°) = 0.5$

So, the equation becomes:

$0.5 = \frac{x}{10}$

Now, multiply both sides by 10 to solve for x:

$x = 0.5 \times 10 = 5 \, \text{cm}$

Final Answer: The length of the side opposite Angle A (30°) is 5 cm.

infoNote

Example 2: Finding an Angle Given Two Sides (Using Cosine)

Problem: In a right-angled triangle, the adjacent side is 8 cm and the hypotenuse is 10 cm. Find Angle A.

Step 1: Identify the sides.

Adjacent side is 8 cm.
Hypotenuse is 10 cm.

Step 2: Choose the ratio. Since the adjacent side and the hypotenuse are involved, and the angle needs to be found, use Cosine:

$\cos(A) = \frac{8}{10}$

Step 3: Solve for Angle A. First, calculate the fraction:

$\cos(A) = 0.8$

To find the angle, use the inverse cosine function on the calculator:

$A = \cos^{-1}(0.8)$

Using the calculator:

$A \approx 36.87°$

What is Inverse Cosine?

The inverse cosine (written as $\cos^{-1}$ ) is used to find the angle when the sides are known. It reverses the cosine function, allowing the calculation of the angle from the ratio of the sides. On a calculator, this is typically accessed by pressing the "shift" or "2nd" button, followed by the cosine function.

Final Answer: Angle A is approximately 36.87°.

infoNote

Example 3: Finding a Side Given an Angle and a Side (Using Tangent)

Problem: In a right-angled triangle, Angle A is 45° and the adjacent side is 7 cm. Find the length of the side opposite Angle A.

Step 1: Identify the sides.

Opposite side is x.
Adjacent side is 7 cm.

Step 2: Choose the ratio. Since the opposite and adjacent sides are involved, and the opposite side needs to be found, use Tangent:

$\tan(45°) = \frac{x}{7}$

Step 3: Solve for x. First, find the value of $\tan(45°)$ using a calculator:

$\tan(45°) = 1$

So, the equation becomes:

$1 = \frac{x}{7}$

Now, multiply both sides by 7 to solve for x:

$x = 1 \times 7 = 7 \, \text{cm}$

Final Answer: The length of the side opposite Angle A (45°) is 7 cm.

infoNote

Exam Tip: Remember SOH-CAH-TOA!

To help remember which sides to use with Sin, Cos, and Tan, use this mnemonic:

SOH: Sine = Opposite / Hypotenuse
CAH: Cosine = Adjacent / Hypotenuse
TOA: Tangent = Opposite / Adjacent In an exam, write down "SOH-CAH-TOA" and use it to figure out which ratio to apply.

Sine, Cosine and Tangent Simplified Revision Notes for Junior Cycle Mathematics

Sine, Cosine and Tangent

What Are Sine, Cosine, and Tangent?

Step 1: Identify the Sides of the Triangle Relative to Angle A

Step 2: Choose the Right Ratio (Sine, Cosine, or Tangent)

Example 1: Finding a Side Given an Angle and a Side (Using Sine)

Example 2: Finding an Angle Given Two Sides (Using Cosine)

Example 3: Finding a Side Given an Angle and a Side (Using Tangent)

Exam Tip: Remember SOH-CAH-TOA!

500K+ Students Use These Powerful Tools to Master Sine, Cosine and Tangent For their Junior Cycle Exams.

Other Revision Notes related to Sine, Cosine and Tangent you should explore