Photo AI
Last Updated Sep 26, 2025
Practice Problems Simplified Revision Notes for Junior Cycle Mathematics
Revision notes with simplified explanations to understand Practice Problems quickly and effectively.
259+ students studying
Practice Problems
Problem
Each of the students in sixth year in a particular school has WhatsApp , Instagram , or Snapchat . The numbers who have each app are as follows:
- 36 students have
- 40 students have
- 54 students have
- 14 students have and
- 24 students have and
- x students have and , but not
- 8 students have all three apps. Questions:
Part (i)****: Use this information to fill in the Venn diagram below, in terms of .
Part (ii): There are 80 students in total in sixth year in the school. Find the value of .
Solutions
Part (i): Filling in the Venn Diagram in Terms of
To solve this problem, we need to place the information given into the Venn diagram, which will show how many students have which apps. Here's how we can do it:
- Start with the center (All three apps):
- 8 students have all three apps ( and ). This number goes right in the center where all three circles overlap.
Exam Tip: Always start by filling in the center of the Venn diagram where all three circles overlap, then work your way outwards. This ensures that you account for students who belong to multiple groups first, making it easier to fill in the remaining sections.
- WhatsApp and Instagram (but not Snapchat):
- 14 students have both and Instagram. Since 8 of these students already use all three apps, we subtract the 8 from 14 to find out how many students only have and .
- So, 6 students only have and (but not ), and this number goes in the overlap between the and circles, but outside the circle.
- Instagram and Snapchat (but not WhatsApp):
- 24 students have both and . Since 8 of these students already use all three apps, we subtract the 8 from 24 to find out how many students only have and .
- So, 16 students only have and (but not ), and this number goes in the overlap between the and circles, but outside the circle.
- WhatsApp and Snapchat (but not Instagram):
- We are told that x students have and , but not . This number x goes in the overlap between the and circles, but outside the circle.
- Total number of students using each app:
-
: 36 students have WhatsApp in total.
-
: 40 students have Instagram in total.
-
: 54 students have Snapchat in total. These totals include all the students who use WhatsApp, Instagram, and Snapchat in any combination (including those who use two or three apps). To find out how many students only use one app, we will need to consider the other overlaps we've already identified.
-
Only WhatsApp: The number of students who only have WhatsApp is calculated by subtracting the number of students who use WhatsApp in combination with Instagram, Snapchat, or both from the total number of WhatsApp users.
-
Only Instagram: The number of students who only have Instagram is calculated by subtracting those who use Instagram in combination with the other apps.
-
Only Snapchat: The number of students who only have Snapchat is found similarly:
In summary, the Venn diagram will be filled as follows:
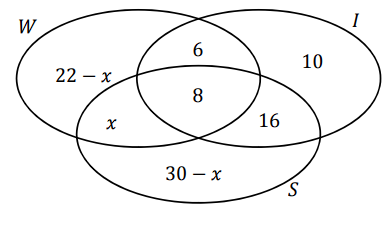
Part (ii): Solving for
In Part (ii), we are told there are 80 students in total. This means that all the numbers in the Venn diagram should add up to 80. We use this information to find the value of x.
-
Write the equation for the total number of students: All the regions in the Venn diagram add up to the total number of students:
-
Simplify the equation: Start by combining like terms:
-
Solve for : To find , subtract 92 from both sides of the equation:
Multiply both sides by -1 to get :
So, the value of is 12.
500K+ Students Use These Powerful Tools to Master Practice Problems For their Junior Cycle Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
120 flashcards
Flashcards on Practice Problems
Revise key concepts with interactive flashcards.
Try Mathematics Flashcards8 quizzes
Quizzes on Practice Problems
Test your knowledge with fun and engaging quizzes.
Try Mathematics Quizzes29 questions
Exam questions on Practice Problems
Boost your confidence with real exam questions.
Try Mathematics Questions27 exams created
Exam Builder on Practice Problems
Create custom exams across topics for better practice!
Try Mathematics exam builder80 papers
Past Papers on Practice Problems
Practice past papers to reinforce exam experience.
Try Mathematics Past PapersOther Revision Notes related to Practice Problems you should explore
Discover More Revision Notes Related to Practice Problems to Deepen Your Understanding and Improve Your Mastery
