Properties of Triangles

Triangles are one of the most basic shapes in geometry, but they have some special rules that make them unique. Understanding these rules will help you solve problems involving triangles, and they're really important for your exams!

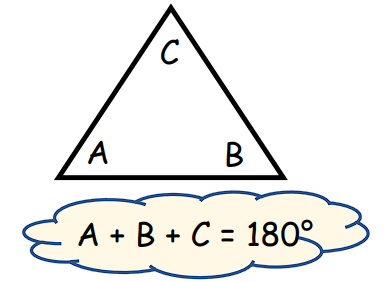
1. The Interior Angles of a Triangle

What You Need to Know: The three angles inside a triangle always add up to 180°. This means that if you know two of the angles, you can easily find the third one by subtracting the sum of the known angles from 180°.
In this triangle, the three angles are labeled $A$ , $B$ , and $C$ . No matter what kind of triangle you have, when you add these angles together, they will always equal 180°. This is a rule that never changes!

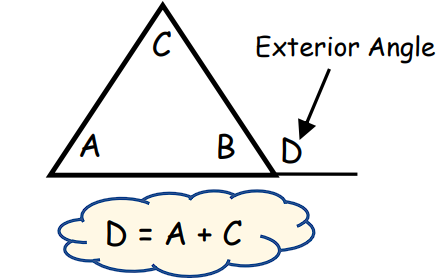
2. The Exterior Angle of a Triangle

What You Need to Know: An exterior angle is formed when you extend one side of the triangle. The cool thing about exterior angles is that they are equal to the sum of the two opposite interior angles.
In this triangle, $D$ is the exterior angle. The rule tells us that $D$ is the same as the sum of the two opposite angles inside the triangle, which are $A$ and $C$ . So, if you know the values of $A$ and $C$ , you can easily find $D$ by adding them together.

Why This Matters

These rules are like shortcuts for solving triangle problems. They're especially helpful in exams because they allow you to quickly figure out missing angles without needing a protractor. Once you understand these properties, you'll find triangles much easier to work with.

Worked Examples

infoNote

Example 1: Finding a Missing Interior Angle

Imagine you have a triangle with two angles given as 50° and 60°. You need to find the third angle.

Step 1: Remember, the interior angles of a triangle always add up to 180°. This is a key rule for triangles.

Why? Because this rule applies to every triangle, it helps you find any missing angle if you know the other two.

Step 2: Add the two given angles:

$50° + 60° = 110°$

Why? Adding these two angles helps us see how much of the total 180° is already used up by these two angles.

Step 3: Subtract this sum from 180° to find the third angle:

$180° - 110° = 70°$

Why? Since all three angles must add up to 180°, subtracting the sum of the known angles from 180° will give you the value of the missing angle.

Answer: The third angle is 70°.

infoNote

Example 2: Using the Exterior Angle Rule

Now, let's say you have a triangle where two of the interior angles are 40° and 70°, and you need to find the exterior angle at one of the vertices.

Step 1: Recall that the exterior angle is equal to the sum of the two opposite interior angles.

Why? This rule tells us that instead of measuring the exterior angle directly, we can simply add the two opposite angles inside the triangle to find it.

Step 2: Add the two opposite angles:

$40° + 70° = 110°$

Why? Adding these two angles gives us the measure of the exterior angle because of the rule that the exterior angle equals the sum of the opposite interior angles.

Answer: The exterior angle is 110°.

infoNote

Tips for Understanding:

Draw Your Own Triangles: It's helpful to draw triangles and practice adding up the angles. Try different shapes and see if the rules still work—they always will!
Memorise the Key Points: Remember that inside a triangle, the angles always add up to 180°, and an exterior angle equals the sum of the two opposite interior angles. These two rules will help you a lot!
Practice, Practice, Practice: The more you practice using these properties, the more comfortable you'll become with triangles.

Properties of Triangles Simplified Revision Notes for Junior Cycle Mathematics

Properties of Triangles

1. The Interior Angles of a Triangle

2. The Exterior Angle of a Triangle

Why This Matters

Worked Examples

Example 1: Finding a Missing Interior Angle

Example 2: Using the Exterior Angle Rule

Tips for Understanding:

500K+ Students Use These Powerful Tools to Master Properties of Triangles For their Junior Cycle Exams.

Other Revision Notes related to Properties of Triangles you should explore