Speed, Distance and Time

Introduction to Speed, Distance, and Time

Speed, distance, and time are three key concepts in understanding how fast something is moving, how far it has traveled, and how long it has been moving.

The relationship between these three quantities can be easily remembered using a simple tool known as the "Speed, Distance, Time Triangle."

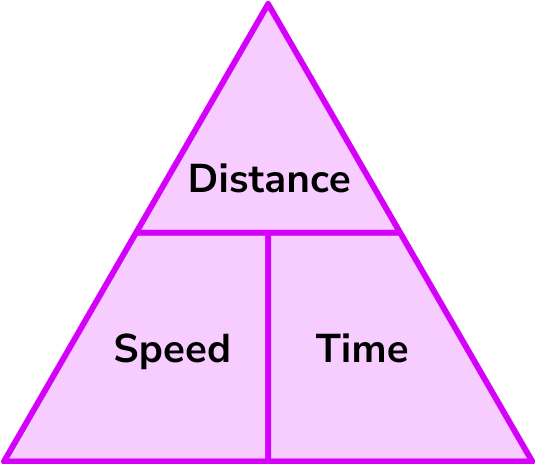
The Speed, Distance, Time Triangle

$D$ stands for Distance.
$S$ stands for Speed.
$T$ stands for Time.

The triangle helps you remember how to calculate one of these quantities if you know the other two.

Using the Triangle to Find Formulas

The triangle is useful because it visually shows the relationship between speed, distance, and time.

Finding Distance $(D)$ :

Cover $D$ in the triangle, and you're left with $S$ × $T$ .
Formula: $\text{Distance} = \text{Speed} \times \text{Time}$
Units: Distance is typically measured in meters ( $m$ ) or kilometers ( $km$ ).

Finding Time $(T)$ :

Cover $T$ in the triangle, and you're left with $D$ ÷ $S$ .
Formula: $\text{Time} = \frac{\text{Distance}}{\text{Speed}}$
Units: Time is usually measured in seconds ( $s$ ) or hours ( $h$ ).

Finding Speed ( $S$ ):

Cover $S$ in the triangle, and you're left with $D$ ÷ $T$ .
Formula: $\text{Speed} = \frac{\text{Distance}}{\text{Time}}$
Units: Speed is commonly measured in meters per second ( $m/s$ ) or kilometers per hour ( $km/h$ ).

Practical Examples

Let's walk through a few examples to understand how to apply these formulas.

infoNote

Example 1: Calculating Distance

Question: A car travels at a speed of $60 km/h$ for $2$ hours. How far does it travel?

Step 1: Identify what you need to find.

We need to find the distance $(D)$ .

Step 2: Use the Speed, Distance, Time Triangle.

Since we are finding distance, cover $D$ in the triangle, leaving us with: $\text{Distance} = \text{Speed} \times \text{Time}$

Step 3: Plug in the values.

Speed = 60 km/h
Time = 2 hours $\text{Distance} = 60 \, \text{km/h} \times 2 \, \text{hours}$

Step 4: Calculate the distance.

$\text{Distance} = :success[120 \, \text{km}]$

So, the car travels 120 km.

infoNote

Example 2: Calculating Time

Question: How long will it take to travel 150 km at a speed of 50 km/h?

Step 1: Identify what you need to find.

We need to find the time (T).

Step 2: Use the Speed, Distance, Time Triangle.

Since we are finding time, cover T in the triangle, leaving us with: $\text{Time} = \frac{\text{Distance}}{\text{Speed}}$

Step 3: Plug in the values.

Distance = 150 km
Speed = 50 km/h $\text{Time} = \frac{150 \, \text{km}}{50 \, \text{km/h}}$

Step 4: Calculate the time. $\text{Time} = :success[3 \, \text{hours}]$

So, it will take 3 hours to travel 150 km.

infoNote

Example 3: Calculating Speed

Question: A cyclist covers 90 km in 3 hours. What is their average speed?

Step 1: Identify what you need to find.

We need to find the speed (S). Step 2: Use the Speed, Distance, Time Triangle.
Since we are finding speed, cover S in the triangle, leaving us with: $\text{Speed} = \frac{\text{Distance}}{\text{Time}}$

Step 3: Plug in the values.

Distance = 90 km
Time = 3 hours $\text{Speed} = \frac{90 \, \text{km}}{3 \, \text{hours}}$

Step 4: Calculate the speed. $\text{Speed} = :success[30 \, \text{km/h}]$

So, the cyclist's average speed is 30 km/h.

Understanding Average Speed

Average Speed is used when an object travels at different speeds over a journey.

It is calculated by dividing the total distance traveled by the total time taken.

$\text{Average Speed} = \frac{\text{Total Distance}}{\text{Total Time}}$

infoNote

Example: A car travels 240 km in 4 hours and then 120 km in 2 hours. What is the car's average speed?

Find the total distance.

Total Distance = 240 km + 120 km = 360 km

Find the total time.

Total Time = 4 hours + 2 hours = 6 hours

Calculate the average speed. $\text{Average Speed} = \frac{360 \, \text{km}}{6 \, \text{hours}} = :success[60 \, \text{km/h}]$

So, the car's average speed is 60 km/h.

Important Tip: Be Careful with Units of Time

When performing these calculations, it's crucial to ensure that all time units are consistent. For example, 1 hour 45 minutes should be converted into hours before using it in the formulas.

Conversion Example:

To convert 1 hour 45 minutes into hours:

$1 \, \text{hour} \, 45 \, \text{minutes} = 1 + \frac{45}{60} \, \text{hours} = :success[1.75 \, \text{hours}]$

This is important because using inconsistent units can lead to incorrect answers.

Recap

Speed, Distance, Time Triangle: A handy tool to remember the formulas for speed, distance, and time.
Distance: Multiply speed by time.
Time: Divide distance by speed.
Speed: Divide distance by time.
Average Speed: Total distance divided by total time.
Always check your units to ensure they are consistent throughout the calculation.

infoNote

Try it out! Question 1: A train travels at a speed of 80 km/h for 3.5 hours. How far does it travel?

Question 2: A cyclist covers 120 km at a speed of 24 km/h. How long does the journey take?

Question 3: A car travels 200 km in 2.5 hours. What is the car's average speed?

Solutions

Question 1: A train travels at a speed of 80 km/h for 3.5 hours. How far does it travel?

Step 1: Identify what you need to find.

We need to find the distance (D) the train travels. Step 2: Use the Speed, Distance, Time Triangle.
Since we are finding distance, cover D in the triangle. This leaves us with the formula: $\text{Distance} = \text{Speed} \times \text{Time}$ Step 3: Plug in the values.
Speed = 80 km/h
Time = 3.5 hours $\text{Distance} = 80 \, \text{km/h} \times 3.5 \, \text{hours}$ Step 4: Calculate the distance. $\text{Distance} = :success[280 \, \text{km}]$

Explanation: We multiplied the speed by the time to find out how far the train travels. The result is 280 km.

So, the train travels 280 km.

Question 2: A cyclist covers 120 km at a speed of 24 km/h. How long does the journey take?

Step 1: Identify what you need to find.

We need to find the time (T) it takes for the cyclist to cover the distance. Step 2: Use the Speed, Distance, Time Triangle.
Since we are finding time, cover T in the triangle. This leaves us with the formula: $\text{Time} = \frac{\text{Distance}}{\text{Speed}}$ Step 3: Plug in the values.
Distance = 120 km
Speed = 24 km/h $\text{Time} = \frac{120 \, \text{km}}{24 \, \text{km/h}}$ Step 4: Calculate the time. $\text{Time} = :success[5 \, \text{hours}]$

Explanation: We divided the distance by the speed to find out how long the journey takes. The result is 5 hours.

So, the journey takes 5 hours.

Question 3: A car travels 200 km in 2.5 hours. What is the car's average speed?

Step 1: Identify what you need to find.

We need to find the speed (S) of the car. Step 2: Use the Speed, Distance, Time Triangle.
Since we are finding speed, cover S in the triangle. This leaves us with the formula: $\text{Speed} = \frac{\text{Distance}}{\text{Time}}$ Step 3: Plug in the values.
Distance = 200 km
Time = 2.5 hours $\text{Speed} = \frac{200 \, \text{km}}{2.5 \, \text{hours}}$ Step 4: Calculate the speed. $\text{Speed} = :success[80 \, \text{km/h}]$

Explanation: We divided the distance by the time to find the average speed. The result is 80 km/h.

So, the car's average speed is 80 km/h.

Speed, Distance and Time Simplified Revision Notes for Junior Cycle Mathematics

Speed, Distance and Time

Introduction to Speed, Distance, and Time

Using the Triangle to Find Formulas

Practical Examples

Example 1: Calculating Distance

Example 2: Calculating Time

Example 3: Calculating Speed

Understanding Average Speed

Example: A car travels 240 km in 4 hours and then 120 km in 2 hours. What is the car's average speed?

Important Tip: Be Careful with Units of Time

Recap

Solutions

500K+ Students Use These Powerful Tools to Master Speed, Distance and Time For their Junior Cycle Exams.

Other Revision Notes related to Speed, Distance and Time you should explore