Transformations

In geometry, a transformation is a way to change the position, size, or shape of a figure. Think of it as a way of moving or flipping a shape around on the page. There are four main types of transformations that you'll need to know about: axial symmetry, central symmetry, translation and rotation. Let's look at each one, using the diagrams provided to help you understand.

1. Axial Symmetry (Reflection)

Axial symmetry happens when a shape is flipped over a line, like looking at yourself in a mirror. The line you flip the shape over is called the axis of symmetry.

• Axial Symmetry in the $X-axis$: Here, the shape is flipped over the $X-axis$ (the horizontal line on the graph). Imagine folding your page along the $X-axis$; the shape ends up on the other side, upside down.

  

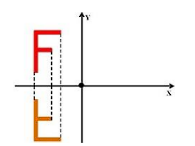
• Axial Symmetry in the $Y-axis$: In this case, the shape is flipped over the $Y-axis$ (the vertical line on the graph). It's like folding the page along the $Y-axis$; the shape moves to the opposite side but stays right side up.

  

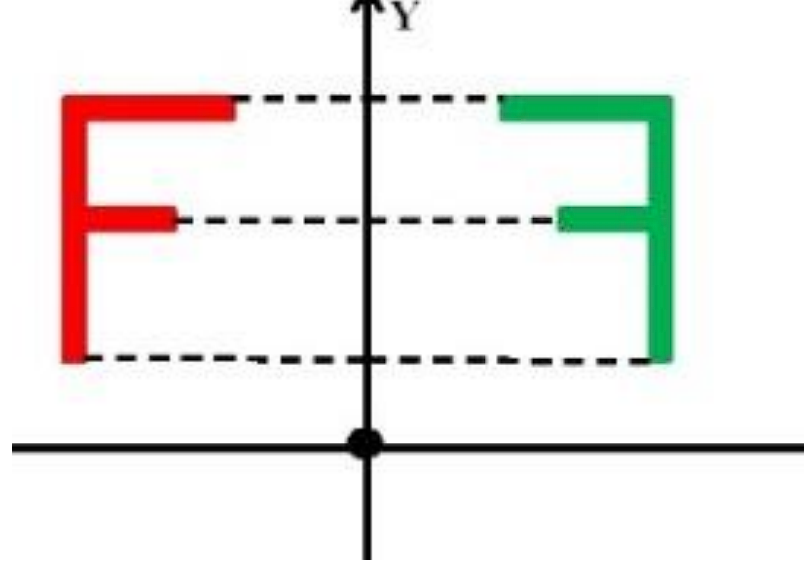
2. Central Symmetry

Central symmetry occurs when a shape is flipped over a point (usually the origin, where the $X-axis$ and $Y-axis$ meet). The shape is rotated 180 degrees, which means it's turned upside down and ends up on the opposite side of the point.

• Central Symmetry in the Origin: When a shape is flipped over the origin, every part of the shape moves to the exact opposite side. For example, a point that was on the top right might end up on the bottom left.

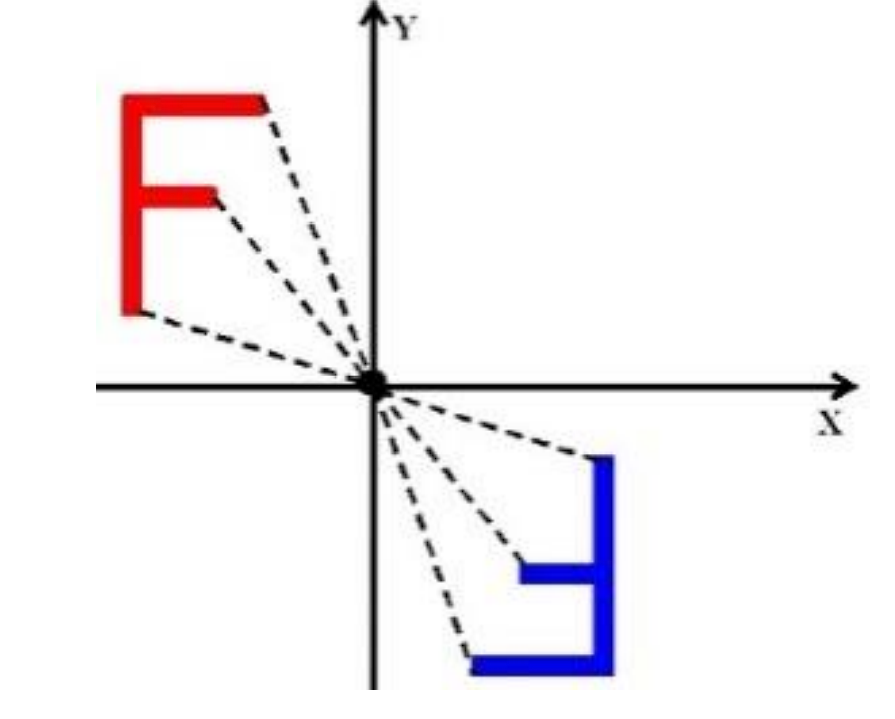
3. Translation

Translation is when you move a shape without rotating it or flipping it. Imagine sliding a book across a table—it's still facing the same way, just in a different place.

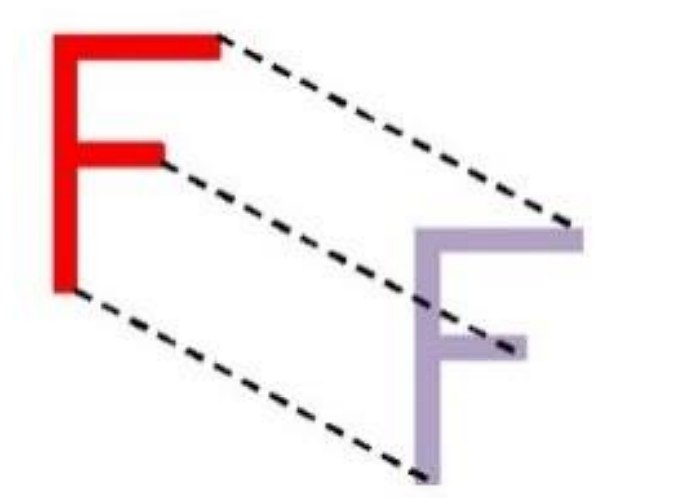
4. Rotation

Rotation means turning a shape around a point, usually the origin. The shape stays the same, but it's turned like a wheel. Common rotations are 90 degrees, 180 degrees, and 270 degrees.

• 90° Rotation: If you turn the shape 90 degrees, it moves to a new position as if you've turned it a quarter turn.
• 180° Rotation: This is like central symmetry. The shape is turned halfway around, so it ends up upside down.
• 270° Rotation: This is a three-quarter turn, so the shape moves to a position as if you turned it 270 degrees.

How to Recognise These Transformations

When you look at a shape and wonder what transformation has happened, here are some clues:

• If the shape looks like it's been flipped over a line, that's a reflection (axial symmetry).
• If the shape is flipped over a point and is upside down, it's central symmetry.
• If the shape has just moved to another spot without flipping, it's a translation.
• If the shape has been turned like a wheel, it's a rotation. Understanding these transformations is key to solving many geometry problems and will help you feel more confident when tackling this topic in your maths exam.