Corollaries of Similar Triangles

Overview

The concept of similarity in triangles leads to several important geometric corollaries. These corollaries establish relationships between side lengths, parallel lines, and areas in similar triangles.

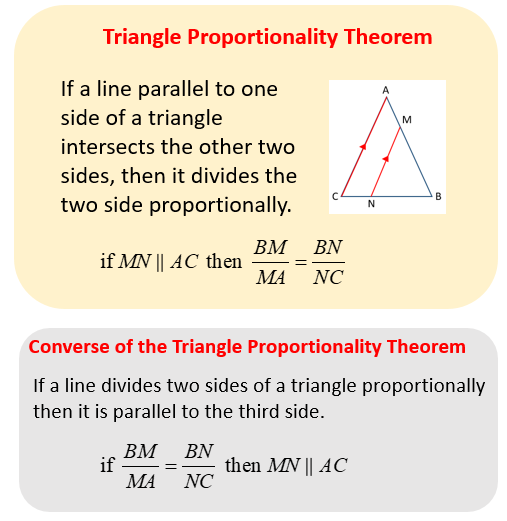
Corollary 5: Line Dividing Two Sides Proportionally

Statement: If a line divides two sides of a triangle proportionally, it is parallel to the third side.
Why It Works:
- By the basic proportionality theorem, a line that divides two sides proportionally creates smaller triangles that are similar to the original triangle.
- The parallel nature of the dividing line follows directly from this similarity.

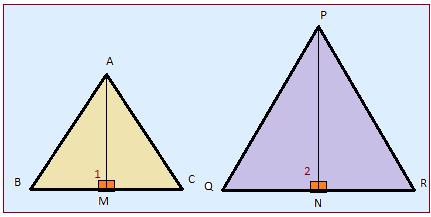
Corollary 6: Ratio of Areas in Similar Triangles

Statement: If two triangles are similar, the ratio of their areas is equal to the square of the ratio of their corresponding sides.

Mathematically:

\frac{\text{Area of } \triangle_1}{\text{Area of } \triangle_2} = \left( \frac{\text{Side of } \triangle_1}{\text{Side of } \triangle_2} \right)^2

Why It Works:

Since similar triangles have proportional sides, their heights are also proportional.
The areas, which depend on both base and height, scale quadratically with the ratio of their corresponding sides.

Worked Examples

infoNote

Example 1: Line Dividing Two Sides Proportionally

Problem: In $\triangle ABC$ , a line $DE$ intersects $AB$ and $AC$ , dividing them such that $\frac{AD}{DB} = \frac{AE}{EC}$

Prove that $DE \parallel BC$

Solution:

By Corollary 5:

If a line divides two sides of a triangle proportionally, it must be parallel to the third side.
Therefore, $DE \parallel BC$

Answer: $DE \parallel BC$

infoNote

Example 2: Ratio of Areas in Similar Triangles

Problem: Two triangles $\triangle ABC$ and $\triangle DEF$ are similar, with corresponding side lengths $AB = 6$ , $DE = 9$ , and $AC = 8$ , $DF = 12$ .

Find the ratio of their areas.

Solution:

By Corollary 6:

The ratio of their areas is equal to the square of the ratio of their corresponding sides:

\frac{\text{Area of } \triangle ABC}{\text{Area of } \triangle DEF} = \left( \frac{AB}{DE} \right)^2 = \left( \frac{6}{9} \right)^2 = \left( \frac{2}{3} \right)^2 = \frac{4}{9}

Answer: The ratio of the areas is $\frac{4}{9}$

Summary

Corollary 5: If a line divides two sides of a triangle proportionally, it is parallel to the third side.
Corollary 6: In similar triangles, the ratio of their areas equals the square of the ratio of their corresponding sides.
These corollaries are essential for solving problems involving proportionality and similarity in geometry.

Corollaries of Similar Triangles Simplified Revision Notes for Leaving Cert Mathematics