Net of a Cone

What is a Net?

A net is a 2D representation of a 3D solid. It shows all the faces of the solid laid flat so that when folded, it forms the solid.

Net of a Cone

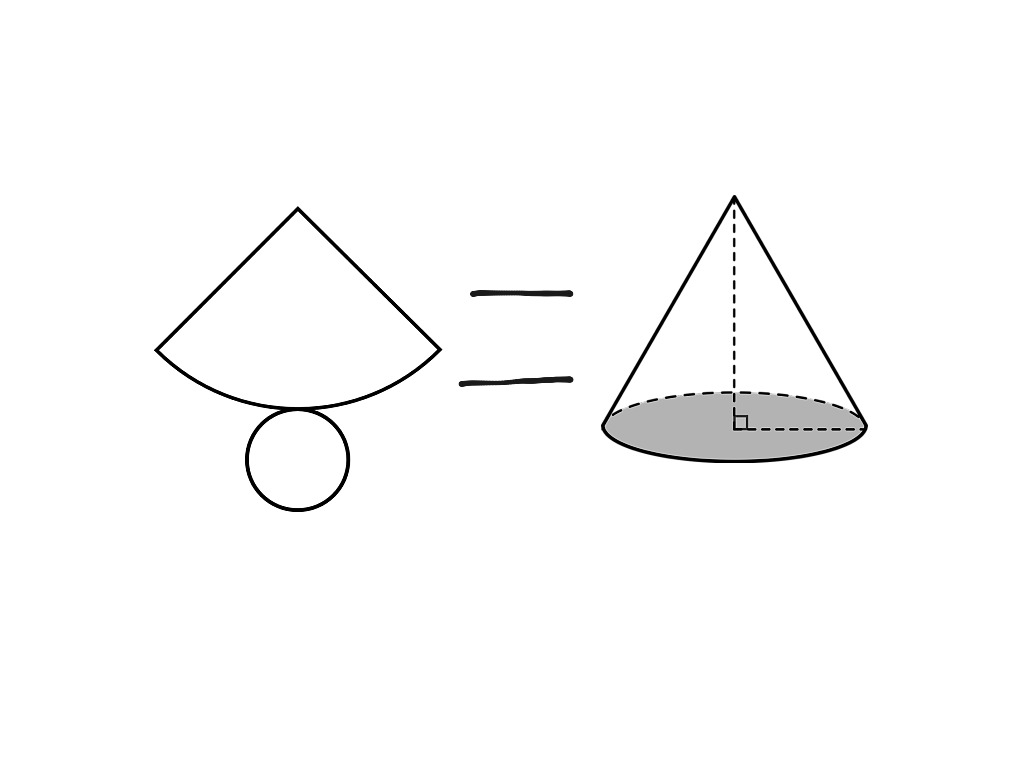
A cone has:

1. A circular base.
2. A curved surface that tapers to a point (vertex). The net of a cone consists of:

• One circle: This represents the base of the cone.
• One sector of a larger circle: This represents the curved surface of the cone. The radius of this larger circle equals the slant height of the cone.

Geometry of the Cone's Net

• Radius of the Base ($r$): The radius of the smaller circle.
• Slant Height ($l$): The radius of the larger circle (sector).
• Angle of the Sector ($\theta$): Determined by the ratio of the cone's base circumference to the circumference of the larger circle: $\theta = \frac{r}{l} \times 360^\circ$

---

Applications of the Cone's Net

Surface Area Calculation:

1. Area of the base: $\pi r^2$
2. Area of the curved surface: $\text{Curved Surface Area} = \pi r l$
3. Total surface area: $\text{Total Area} = \pi r^2 + \pi r l$

---

Worked Example

---

---

Summary

• Net of a Cone: Includes a circular base and a sector for the curved surface.
• Key Formulae:
  1. Curved Surface Area: $\pi r l$
  2. Total Surface Area: $\pi r^2 + \pi r l$
• Applications: Useful for geometry problems involving surface area and for creating accurate models of cones.