Differentiating Expressions

Introduction

Differentiation is a fundamental concept in calculus that deals with the rate at which a function changes. It is the process of finding the derivative of a function, which represents the slope of the function's graph at any given point.

If $f(x)$ is a function, the $f'(x)$ is the derivative of that expression.

The following animation represents the different points of the first derivative of the function $f(x)=x \sin(x^2)+1$. At steep regions, the slope is also steep, and at shallow or flat regions, the slope is also shallow or flat.

---

---

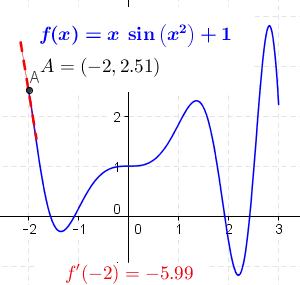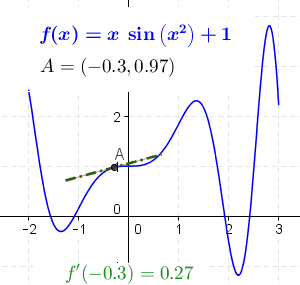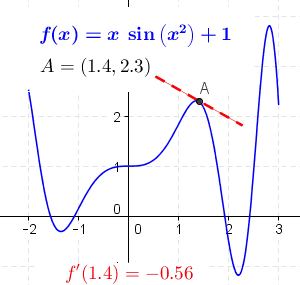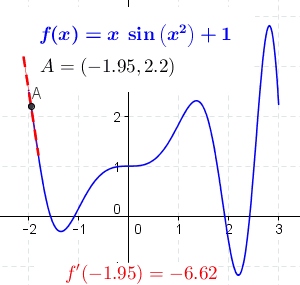
Differentiating by Terms

The simplest form of differentiation is differentiating term by term. Informally, we multiply the power of that term with the coefficient and subtract $1$ from the power. In general :

$$f(x)=ax^n \implies f'(x)=anx^{n-1}$$

Example

Example

Example

Example

Example