Photo AI
Last Updated Sep 27, 2025
Terminology Simplified Revision Notes for Leaving Cert Mathematics
Revision notes with simplified explanations to understand Terminology quickly and effectively.
291+ students studying
Terminology
Algebra is a branch of mathematics that deals with symbols and the rules for manipulating these symbols. It is the basis of the Leaving Certificate mathematics course as every subsequent chapter requires a sufficient understanding of algebraic topics.
Terminology
It is recommended you develop a good understanding of the algebraic terminology as they will reappear commonly in subsequent chapters.
A constant is a fixed value that does not change. For instance, 4 is a constant since the number 4 will always be that value.
A variable is a symbol that represents an unknown value. In mathematics, we typically denote variables as letters such as or .
A coefficient is a number that multiplies a variable. It tells you how many times the variable is being added or subtracted. For example, In the expression , the coefficient is . In other words, we multiply four times ()
A term is a single component of an expression. They can be constants, variables or terms. Terms are always separated by or .
An expression is a combination of terms involving variables, constants and operations. For example is an expression.
An equation is a mathematical statement that shows two expressions are equal, for example .

Operations
Operations are the essence of any algebraic system and mastering their relationship with other operations is crucial in understanding algebra.
Addition and Subtraction
In algebra, only like terms can be added or subtracted.
Two terms are like terms if they have the same variable with the same degree (power).
-
and are like terms, they share the same variable raised to the same power .
-
and are like terms, any constants are like terms of each other.
-
and are like terms, they share same combination of variable to the same power.
-
and are like terms
-
and -7$$y are not like terms, they don't share the same variable name.
-
and are not like terms, they share the same variable but not raised to the same power.
-
and are not like terms, they don't share the same combination are like terms.
When adding or subtracting like terms, only sum their coefficients. For example .
For example, let's simplify the expression :
First identify all the like terms. There are three terms.
There are two terms,
There are two constant terms,
This is the simplified expression, the simplest form is when no more like terms can be added.
Addition is commutative, meaning it doesn't matter in which order we arrange addition, for example is the same value as .
Subtraction is not commutative, but subtraction can be written in terms of addition. For example, if we wanted to rearrange :
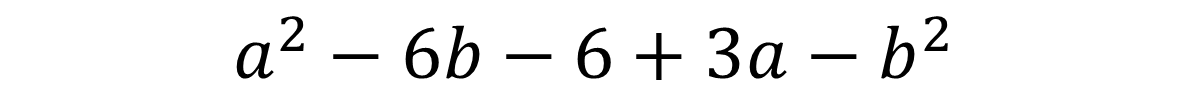
Rewrite in terms of addition (the sign is always attached to the term)
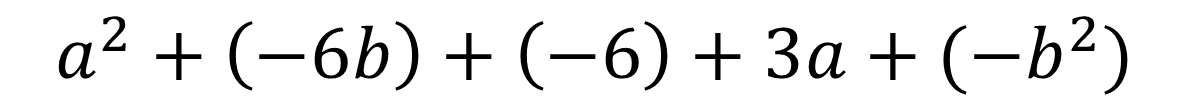
Rearrange using the commutative law of addition.
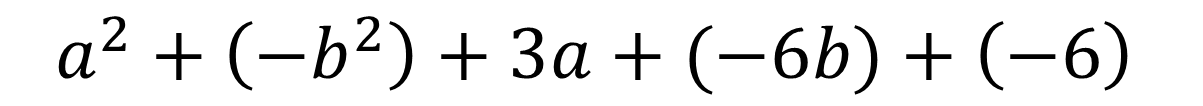
Remove brackets :
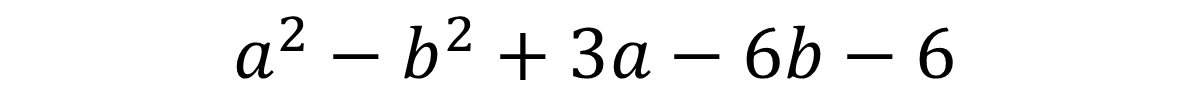
Multiplication
Multiplication does not concern itself with like terms, we can simply follow basic multiplication rules, multiply constants with constants, variables with variables etc.
When multiplying variables, we follow indices rules, when the base is the same but the power is different, add the powers together.
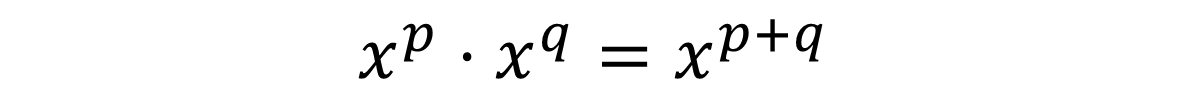
Let's have a look at some examples :
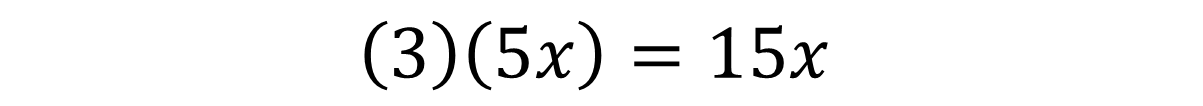
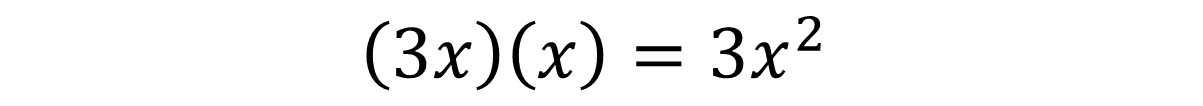
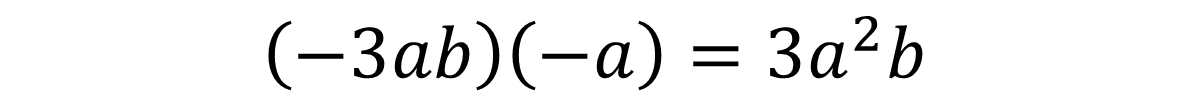
Multiplication has an interesting property when paired with addition of subtraction, the law of distribution.
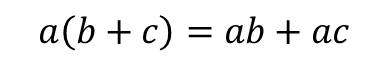
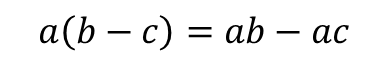
This law is very powerful because it let's us expand brackets. That is, when we want to multiply two brackets, the first bracket distributes amongst each term in the second bracket.
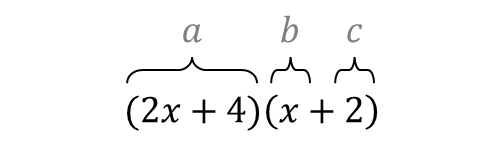
Now distribute amongst and .
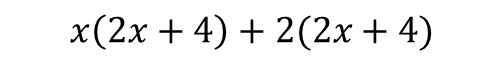
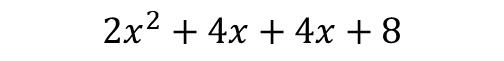
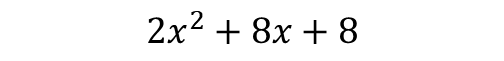
Division
Similar to multiplication, we handle respective components, divide coefficients and subtract exponents where applicable. We refer to the indices rules again :
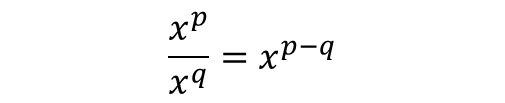
Division is synonymous with fractions, and using them interchangeably is key to understanding algebra, especially when dealing with fractions. When expressing division, we use fraction notation instead of or .
A key property of fraction is that when the numerator and denominator share a common factor, it cancels out :
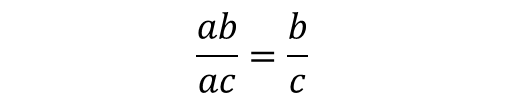
Let's explore some examples :
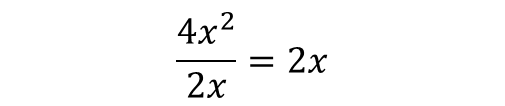
Recall we handle components separately, so the constants divide () and the -terms divide, using indices rules.
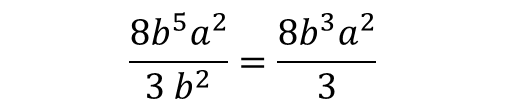
and don't divide evenly so we can leave those untouched if we want to avoid decimal notation. The -terms are handled using indices rules and the term doesn't have anything to cancel out with on the bottom of the fraction, so this stays unaffected.
Algebraic long division will be explored in a later chapter.
Indices
In the same way multiplication represents repeated adding, exponents represent repeated multiplication.
Indices have their own unique properties - two of which we've already seen. We'll explore the rest in a subsequent section.
Let's have a look at an example for now :
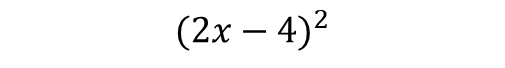
This expression says that we repeatedly multiply twice, so let's rewrite it in multiplicative form :
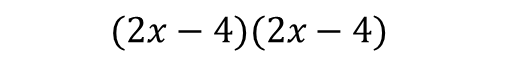
From here we should know what to do, try it as an exercise.
Precedence of Operations
So far we have met the five basic operations of algebra - addition, subtraction, multiplication, division and exponentiation (or indices). Some operations come before others, we can refer to BIMDAS to see which ones to do first.

Let's work through an example :
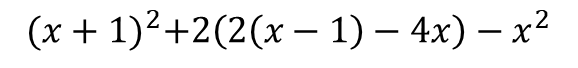
First we handle brackets - start with the most nested bracket
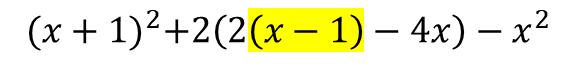
Nothing to simplify, onto the other bracket :
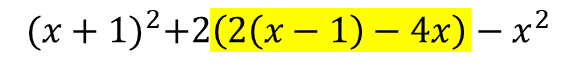
In here, we can simplify
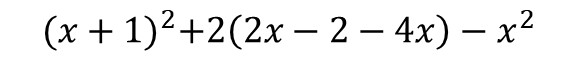
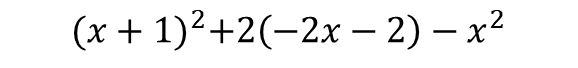
There's nothing left to simplify in the brackets, we move onto indices :
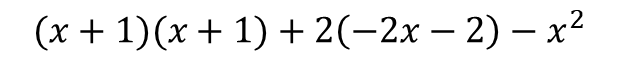
Next is multiplication :
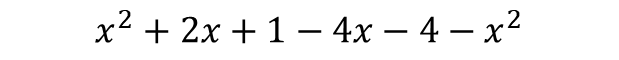
Addition and subtraction actually have the same precedence, clean up the expression from left to right :
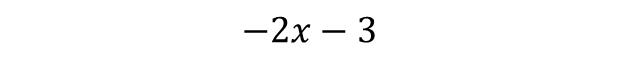
500K+ Students Use These Powerful Tools to Master Terminology For their Leaving Cert Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
250 flashcards
Flashcards on Terminology
Revise key concepts with interactive flashcards.
Try Mathematics Flashcards16 quizzes
Quizzes on Terminology
Test your knowledge with fun and engaging quizzes.
Try Mathematics Quizzes29 questions
Exam questions on Terminology
Boost your confidence with real exam questions.
Try Mathematics Questions27 exams created
Exam Builder on Terminology
Create custom exams across topics for better practice!
Try Mathematics exam builder322 papers
Past Papers on Terminology
Practice past papers to reinforce exam experience.
Try Mathematics Past PapersOther Revision Notes related to Terminology you should explore
Discover More Revision Notes Related to Terminology to Deepen Your Understanding and Improve Your Mastery
