Entropy and Gibbs Energy

Introduction to Thermodynamics

Basic Concepts

• System: The section of the universe being studied.
• Surroundings: All external aspects interacting with the system.
• Universe: The total of the system and surroundings.

Laws of Thermodynamics

• First Law (Conservation of Energy): Energy cannot be created or destroyed, only converted from one form to another.

  • Example: When a system performs work, like gas compression, its internal energy decreases.

• Second Law: Entropy of an isolated system will never decrease over time.

  • Example: Refrigerators facilitate heat transfer from colder to warmer areas, increasing total system entropy.

• Third Law: At absolute zero, the entropy of a perfect crystal is zero, reflecting complete molecular order.

  • Mathematical Clarity: $S = 0$.

Distinctions Between Energy Types

• Energy: The ability to perform work or generate heat.
• Thermodynamic Energy: Comprises particular energies like enthalpy (heat content) and Gibbs Free Energy (potential for spontaneity).

Foundation for Further Study

• A grasp of entropy, enthalpy, and Gibbs Free Energy is vital for evaluating reaction spontaneity and deeper thermodynamic concepts.
• Lays groundwork for advanced studies including the significance of Gibbs Free Energy.

Visual Aid

Integrating these fundamental concepts enables students to approach complex topics like Gibbs Free Energy and its role in chemical reactions.

---

Entropy: A Measure of Disorder

Key Concepts and Definitions

• Entropy (S):
  • Definition: A metric of a system's energy unavailable for useful work.
  • Significance: Reflects energy spread within a system.
  • Units: Measured in Joules per Kelvin (J/K), quantifying energy unavailability.

Entropy and Disorder

• Correlation with Disorder:
  • Entropy Quantification: Evaluates how disorder and energy spread are measured within a system.
  • Common Misconception: Highlights that entropy encompasses more than disorder, representing the extent of energy distribution.

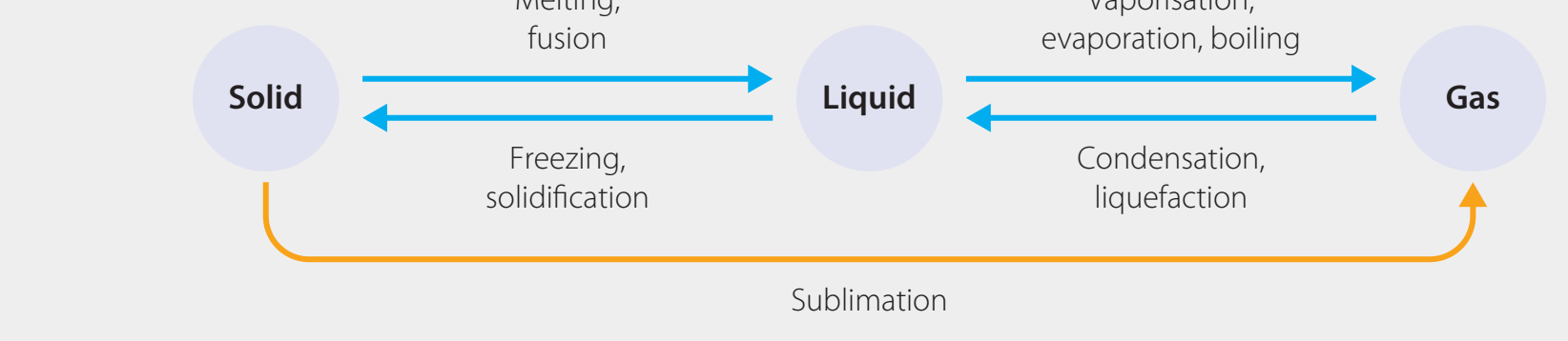
Entropy Change During Phase Transitions

• Phase Transitions and Reactions:
  • Transitions from solid to liquid to gas involve increased entropy:
    • Solid to Liquid: Entropy rises as solid structures dissolve.
    • Liquid to Gas: Entropy further increases as molecules disperse upon vaporisation.
  • Entropy Change Formula ($\Delta S$): Apply $\Delta S = \frac{\Delta Q}{T}$, emphasising formula application to reinforce understanding.

Examples of Entropy Changes

• Practical Examples:
  • Melting Ice: Demonstrate the process with straightforward energy absorption leading to disorder rise and transition to liquid.
    • Calculation Example: Follow a step-by-step process using $\Delta S = \frac{\Delta Q}{T}$ for 1 mole of ice.
  • Dissolving Salt in Water: Describe how entropy increases as particles spread, showcasing increased randomness.

Visual Representation

• Diagrams and Models:
  • Explicitly reference diagrams to assist application.

Important Concepts and Highlights

• Key Points to Highlight:
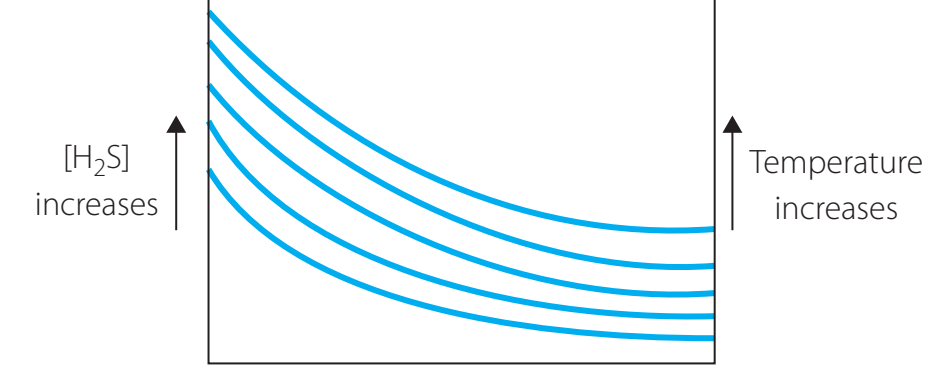
  • Temperature's Effect on Entropy: Increasing temperatures typically elevate entropy, enhancing energy distribution.
  • Irreversible Processes: Numerous natural processes are irreversible since they result in a net rise in entropy.

Summary

• Grasping entropy is essential for understanding energy interactions in thermodynamics.
• Core Functionality: Entropy is key in anticipating phase changes and spontaneous reactions.
• Misconceptions and Realities: Dispel the notion that entropy simply denotes disorder, underscoring its broad role in energy distribution.

---

Enthalpy: Understanding the Heat Content

Key Concepts

• Enthalpy (H): Complete heat content within a system.
• Formula: $H = U + PV$, where $U$ is internal energy and $PV$ is pressure-volume work.
• Units: Joules (J).

Understanding Enthalpy Changes

• Introduction to ΔH: ΔH quantifies heat uptake or release during reactions.
  • Analogy: Similar to ice melting (heat uptake) or wood burning (heat release).
• Equation: $\Delta H = \Delta U + P\Delta V$, where $\Delta U$ indicates change in internal energy and $P\Delta V$ represents work done.

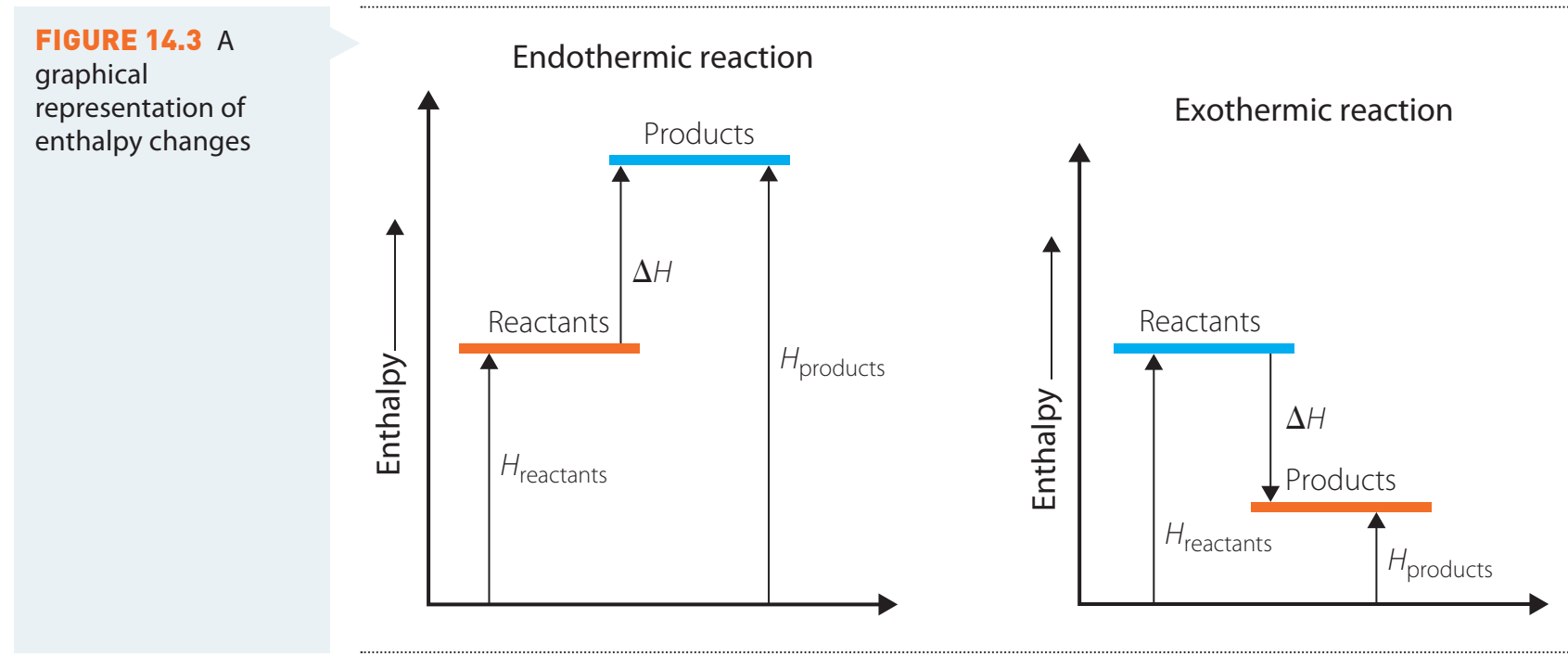
Exothermic vs. Endothermic Reactions

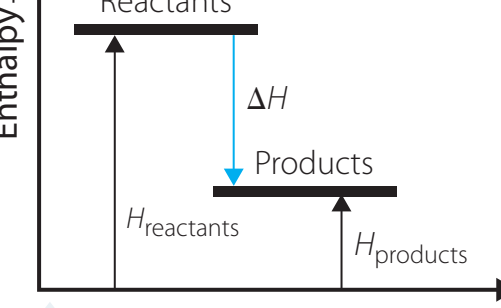
• Exothermic Reactions:

  • Definition: Process that releases heat, producing a negative ΔH.
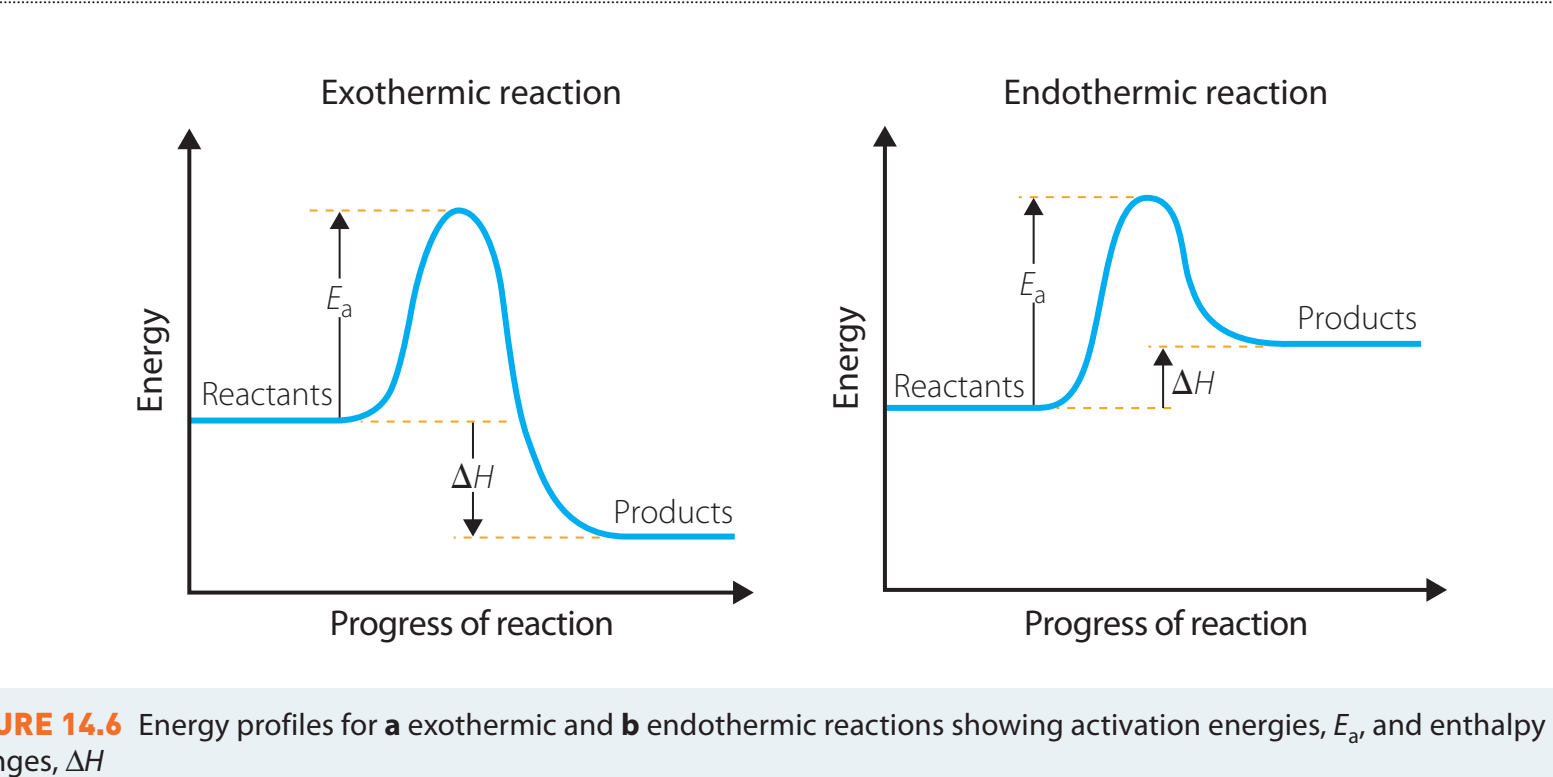
    • Diagram Interpretation: Initial energy input represents activation energy, with a lower final state indicating heat release.

• Endothermic Reactions:

  • Definition: Processes that absorb heat, yielding a positive ΔH.
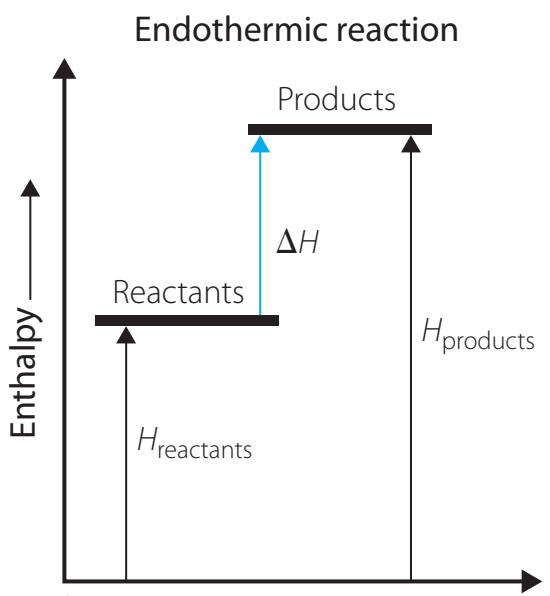
    • Diagram Interpretation: A rising energy profile signifies an increase in heat.

• Standard State Conditions: Measurements taken at 298K, 1 atm.

Practical Examples and Calculations

• Example Walkthrough:
  • Calculate ΔH using Hess's Law:
    1. Deconstruct the total reaction into stages.
    2. Utilise known ΔH values for each stage to ascertain total ΔH.

Highlights and Key Points

• State Function Highlight: ΔH depends solely on initial and final states. Vital for studying thermodynamic properties.
• Exact Correspondence Callout: ΔH = q_p, indicating heat at constant pressure.

Misconceptions Clarified

• Common Errors:
  • Confusing H with heat itself.
  • Clarification: $\Delta H = q_p$ (heat under constant pressure).
• Assumptions:
  • Erroneously linking higher enthalpy with stronger chemical bonds.

Tables/Charts

Reaction	ΔH (kJ/mol)
Combustion of methane	-890.3
Formation of water	-241.8

Table: Compare reactions under standard conditions showcasing ΔH values.

1. Introduction to Entropy vs. Enthalpy

• Entropy (S): Effect of energy dispersion within a system.
• Enthalpy (H): Comprehensive heat content at constant pressure.
• Core Question: How do these concepts differ and interact?

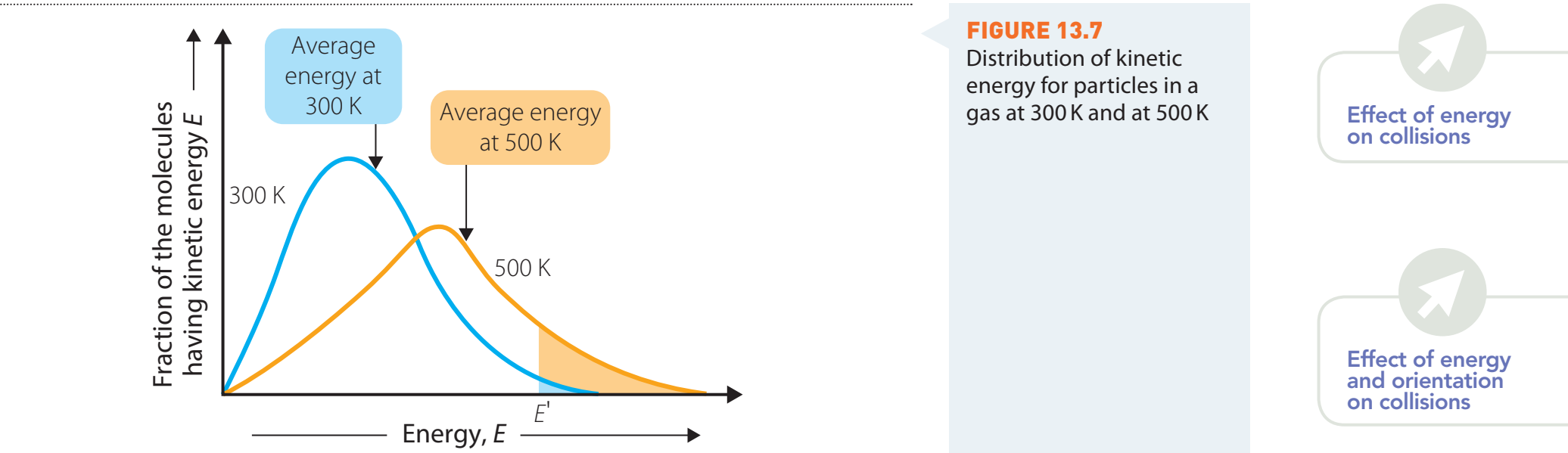
2. Entropy as Energy Dispersal

• Describes: The extent of energy dispersion within a system.
• Higher Entropy: Reflects extensive energy spread.
• Example: Gas expansion into a vacuum indicates rising entropy.

3. Enthalpy as Heat Content

• Measures: Total heat within a system under constant pressure.
• Includes: Internal energy and shifts in pressure-volume tasks.
• Examples: Cooling coffee and combustion illustrate enthalpy.

4. Comparing Energy Level Diagrams

• Diagrams Showcase: Exothermic vs. Endothermic processes.
• Energy Shifts: Visualised regarding both entropy and enthalpy.

Gibbs Free Energy: Combining Entropy and Enthalpy

Introduction

• Objective: Highlight how Gibbs Free Energy predicts reaction spontaneity by integrating entropy and enthalpy.
• Explanation: Gibbs Free Energy (G) calculates a balance between enthalpy (H) - total heat content, and entropy (S) - disorder within a system.

Fundamental Equation

• Formula Analysis: $G = H - TS$
  • H: Enthalpy (Heat content)
  • T: Temperature (Kelvin required)
  • S: Entropy (Degree of disorder)

Derivation of $ΔG = ΔH - TΔS$

• Step-by-step Derivation:
  • Begin with the equation $ΔG = ΔH - TΔS$.
  • Connect $\Delta G$, $\Delta H$, and $\Delta S$ to energy and disorder changes.
  • Recognise each component's effect on reaction viability.

Gibbs Free Energy and Spontaneity

• Reaction Predictions:
  • Spontaneous: $ΔG < 0$
  • Equilibrium: $ΔG = 0$
  • Non-spontaneous: $ΔG > 0$
• Temperature's Role: Temperature influences the TS term, affecting reaction spontaneity.

Illustrative Examples

• Example Calculations:
  • Compute $ΔG$ with given data: $ΔH = 100 kJ/mol$, $T = 298 K$, $ΔS = 200 J/K\cdot mol$.
    • Convert $ΔS$ units from J to kJ: $200 J/K\cdot mol = 0.2 kJ/K\cdot mol$.
    • Substitute into $ΔG = ΔH - TΔS$.
    • Calculate: $ΔG = 100 - (298 \times 0.2) = 40.4 kJ/mol$.

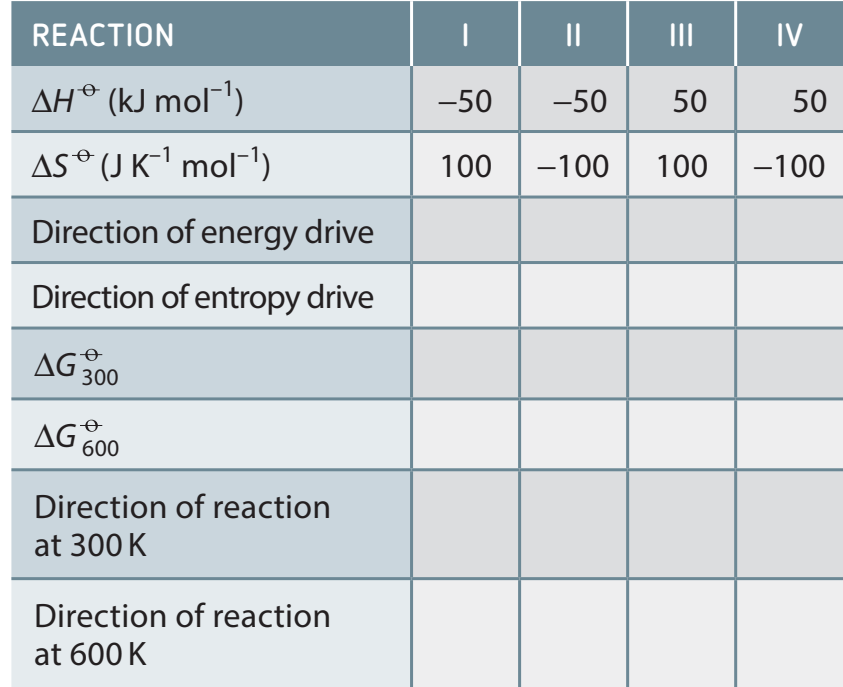
Importance of Temperature

• Scenario Analysis:
  • Assess how temperature affects $ΔG$ using graphical scenarios.

5. Interconnections

• Equation Used: Gibbs Free Energy, $ΔG = ΔH - TΔS$.
• Spontaneity Predictor: Assesses whether reactions occur spontaneously.
• Component Breakdown: $\Delta G$ assesses spontaneity, $\Delta H$ is heat-related, $T\Delta S$ involves entropy.
• Worked Example: Evaluate $\Delta G$ to demonstrate reaction options and spontaneity.

Key Concepts and Highlights

• Entropy: Concerns the distribution of energy throughout systems.
• Enthalpy: Relates to a system's heat content under constant pressure.
• Potential Test Question: Given $\Delta H$ and $\Delta S$ values, compute $\Delta G$ and assess reaction spontaneity.

Clarifying Misconceptions

Introduction to Misconceptions

In thermodynamics, abstract concepts like entropy and enthalpy often lead to misunderstandings. Comprehending these terms is crucial for academic and practical applications.

Misconception about Entropy

• Misconception 1: Entropy as a measure of disorder.
  • Clarification: Entropy measures energy dispersal rather than solely disorder.
  • Example: Entropy increases when ideal gases mix, with no visible disorder change.
  • Key Concept: Microstates and statistical mechanics explain entropy increases without evident disorder variations.

• Misconception 2: ΔS is always positive.
  • Clarification: ΔS can be negative, as in gas to liquid condensation where molecules arrange orderly.

Misconception about Enthalpy

• Misconception 3: Enthalpy change (ΔH) concerns only heat.

  • Clarification: ΔH includes internal energy changes and work, expressed as: $\Delta H = \Delta U + P\Delta V$
  • Example: Pressure-volume work matters in gases; an expanding gas in a cylinder is a case.

• Misconception 4: Standard enthalpy changes are consistent.

  • Clarification: Temperature and pressure significantly impact standard enthalpy values.

Examples and Reinforcement

• Worked Example: Calculate ΔS for condensation. Given: Initial state = gas, Final state = liquid;
  • Calculation: Use relevant formulas to detail changes.
  • Explanation: A detailed guide presents practical application.

---

Worked Examples

Example 1: Entropy Calculation

Scenario: Ice melts into water at 0°C.

• Steps:

  1. Calculate energy: $Q_{rev} = 334 \times 18$ J.
  2. Apply formula: $ΔS = \frac{Q_{rev}}{273}$.
  3. Interpretation: Importance of increased randomness as ice melts.

• Result Statement: Entropy change is 22.05 J/K/mol.

Example 2: Enthalpy Change

Reaction: Combustion of methane.

• Steps:
  • Compute energy for bond breakage/formation separately.
  • Differentiate between energy usage and release.
  • Analyse with Energy Profile Diagram.

Example 3: Gibbs Free Energy

Scenario: Water decomposition at 500K.

• Steps:
  • Calculate $ΔG$ using $ΔH - TΔS$.
  • Highlight impact on spontaneity with temperature variation.
  • Real-life application in natural spontaneous reactions.

---

Practice Questions

Question 1: Entropy Change

Context: Gas expansion in a sealed container.

• Consider how volume change affects entropy: 10 L to 20 L at 298 K.

Solution:

• For an ideal gas expanding isothermally, entropy change can be calculated using: $ΔS = nR\ln(V_2/V_1)$
• Given: $V_1 = 10$ L, $V_2 = 20$ L, $T = 298$ K
• If we assume 1 mol of gas: $ΔS = 1 \times 8.314 \times \ln(20/10) = 5.76$ J/K

Question 2: Enthalpy in Non-standard Conditions

Framework: Reaction at 2 atm pressure, 300 K.

• Calculate $ΔH$ under these specific circumstances.

Solution:

• For a reaction at non-standard conditions, we must consider pressure effects.
• If the reaction involves gases, $ΔH$ varies with pressure according to: $ΔH_{P_2} = ΔH_{P_1} + Δn_{gas}RT\ln(P_2/P_1)$
• If $ΔH_{1atm} = -100$ kJ/mol and $Δn_{gas} = -1$ mol: $ΔH_{2atm} = -100 + (-1)(8.314 \times 10^{-3})(300)\ln(2/1) = -101.73$ kJ/mol

Question 3: Gibbs Energy in Metabolic Process

Scenario: Feasibility in cells at 310K.

• Use Gibbs Free Energy equation to examine metabolic reaction conditions.

Solution:

• For a metabolic reaction with $ΔH = 30$ kJ/mol and $ΔS = 100$ J/K·mol:
• $ΔG = ΔH - TΔS = 30 - (310 \times 0.100) = 30 - 31 = -1$ kJ/mol
• Since $ΔG < 0$, the reaction is spontaneous at body temperature (310K).
• This demonstrates how some metabolic reactions become favourable at physiological temperatures despite being endothermic.

---