Photo AI
Last Updated Sep 27, 2025
Simple harmonic motion (SHM) Simplified Revision Notes for A-Level AQA Physics
Revision notes with simplified explanations to understand Simple harmonic motion (SHM) quickly and effectively.
361+ students studying
6.1.2 Simple harmonic motion (SHM)
Simple Harmonic Motion (SHM) describes the motion of an object that oscillates back and forth along a straight line. An object is said to be in simple harmonic motion when its acceleration is directly proportional to its displacement from a central equilibrium position and acts in the opposite direction to the displacement.
The key equation for SHM is:
Where:
- = acceleration
- = angular speed
- = displacement from equilibrium This equation shows that as the displacement increases, the acceleration also increases but in the opposite direction, always pointing back towards the equilibrium position.
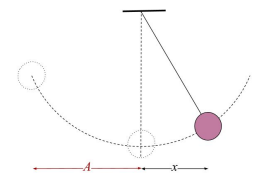
Example of Simple Harmonic Oscillator: Pendulum Motion
Consider a simple pendulum, which is a classic example of SHM. The pendulum oscillates around a central midpoint known as the equilibrium position.
- Displacement measures how far the pendulum is from this midpoint.
- Amplitude ( is the maximum distance (or displacement) from the equilibrium position that the pendulum reaches during its swing.
To analyse the SHM of the pendulum, we can measure:
- The displacement of the pendulum at any point.
- The time period , which is the time taken for the pendulum to complete a full oscillation (back and forth to the equilibrium and back).
Formulas for Simple Harmonic Motion
- Displacement as a function of time:
where is time.
- Velocity ( can be derived from displacement:
This indicates that the velocity is maximum when (at the equilibrium) and zero when (at the amplitude).
- Acceleration is derived from velocity:
Here, acceleration is directly proportional to displacement but in the opposite direction.
Graphical Representation of SHM
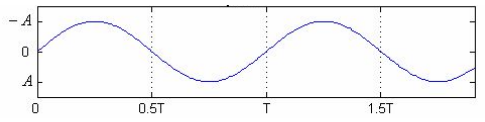
- Displacement-Time Graph: The displacement graph is a cosine or sine curve oscillating between and . This shows the object's back-and-forth motion with a periodic maximum displacement.
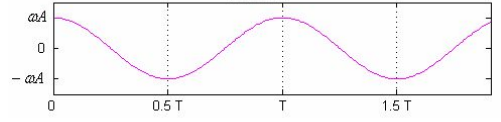
- Velocity-Time Graph: The velocity-time graph is derived as the gradient of the displacement-time graph. It oscillates between and , with velocity being zero at maximum displacement points and maximum at the equilibrium position.
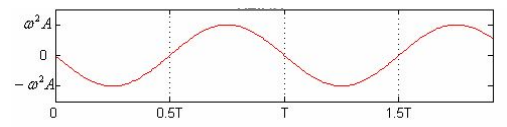
- Acceleration-Time Graph: The acceleration graph, derived from the gradient of the velocity-time graph, oscillates between and . The maximum acceleration occurs when the displacement is maximum, as seen in the equation .
Key Characteristics of SHM
- Maximum Speed:
- Maximum Acceleration:
In simple harmonic motion, the energy of the oscillator continually shifts between kinetic energy (when the object passes through the equilibrium) and potential energy (when it reaches the maximum displacement).
500K+ Students Use These Powerful Tools to Master Simple harmonic motion (SHM) For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
40 flashcards
Flashcards on Simple harmonic motion (SHM)
Revise key concepts with interactive flashcards.
Try Physics Flashcards4 quizzes
Quizzes on Simple harmonic motion (SHM)
Test your knowledge with fun and engaging quizzes.
Try Physics Quizzes29 questions
Exam questions on Simple harmonic motion (SHM)
Boost your confidence with real exam questions.
Try Physics Questions27 exams created
Exam Builder on Simple harmonic motion (SHM)
Create custom exams across topics for better practice!
Try Physics exam builder56 papers
Past Papers on Simple harmonic motion (SHM)
Practice past papers to reinforce exam experience.
Try Physics Past PapersOther Revision Notes related to Simple harmonic motion (SHM) you should explore
Discover More Revision Notes Related to Simple harmonic motion (SHM) to Deepen Your Understanding and Improve Your Mastery
