6.1.3 Simple harmonic systems

Examples include:

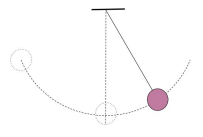
Simple Pendulum: A small, dense bob of mass $m$ hangs from a string of length $l$, fixed at one end. When displaced by a small angle $($less than $:highlight[10^\circ])$, the bob will oscillate in SHM.

• Formula for Time Period $( T )$:

$$T = 2\pi \sqrt{\frac{l}{g}}$$

• where $T$ is the time period, $l$ is the string length, and $g$ is the acceleration due to gravity.
• Conditions for Validity: This formula assumes small angle approximation (less than $:highlight[10^\circ]$). For larger initial angles, this approximation fails, and SHM is not an accurate model.
• Energy Transfer in SHM: During oscillation, the pendulum's energy oscillates between gravitational potential energy and kinetic energy as it moves back and forth through the equilibrium position.

Mass-Spring System: Consists of a mass attached to a spring that can oscillate either vertically or horizontally.

• Formula for Time Period $( T )$:

$$T = 2\pi \sqrt{\frac{m}{k}}$$

Where $m$ is the mass and $k$ is the spring constant.

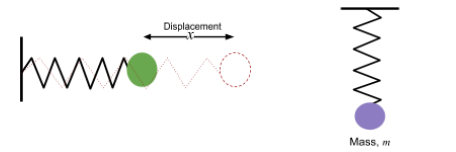
Energy Transfer: In vertical motion, energy oscillates between elastic potential energy (in the spring) and gravitational potential energy. In horizontal motion, energy oscillates solely between elastic potential energy and kinetic energy.

Energy Transformation in SHM:

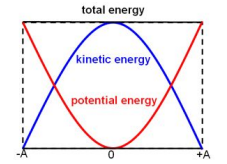
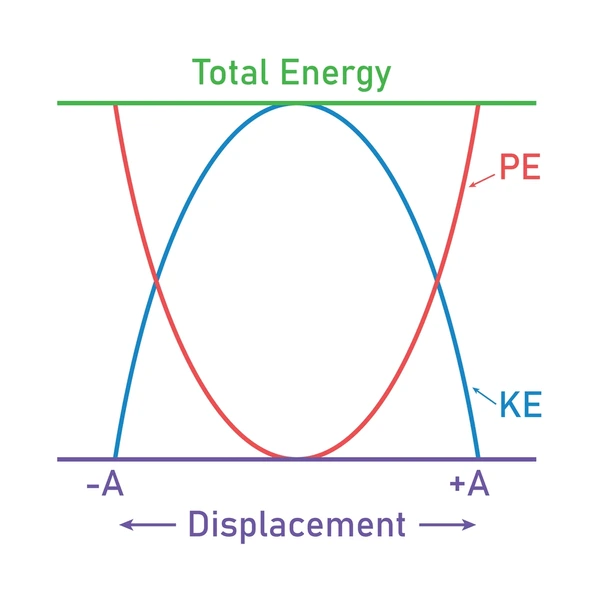
For any simple harmonic system:

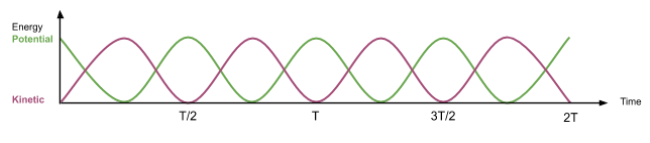
• Kinetic Energy (KE) and Potential Energy (PE) interchange as the system oscillates.
• At maximum displacement (amplitude), potential energy is at its peak, while kinetic energy is zero.
• At the equilibrium position, kinetic energy is maximum, and potential energy is minimum.
• Total energy remains constant (assuming negligible air resistance).

The following graphs illustrate these energy changes:

• Energy vs Displacement graph shows potential and kinetic energies oscillating with displacement.

  

• Energy vs Time graph shows these energy forms alternating with time.

Damping in SHM:

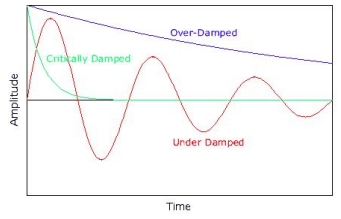
Damping is the gradual loss of energy to the environment, causing the oscillation's amplitude to decrease. Types of damping include:

1. Light Damping (Under-damping): Amplitude reduces slowly over time.
2. Critical Damping: Amplitude decreases to zero in the shortest possible time without further oscillation.
3. Heavy Damping (Over-damping): Amplitude decreases to zero without oscillation, but more slowly than in critical damping. Each type of damping affects how quickly oscillations fade, as shown in amplitude-time graphs for different damping levels.

This topic highlights key principles of simple harmonic systems and how energy dynamics, time periods, and damping influence oscillatory behaviour in mechanical systems.