Photo AI
Last Updated Sep 27, 2025
Circular motion Simplified Revision Notes for A-Level AQA Physics
Revision notes with simplified explanations to understand Circular motion quickly and effectively.
213+ students studying
6.1.1 Circular motion
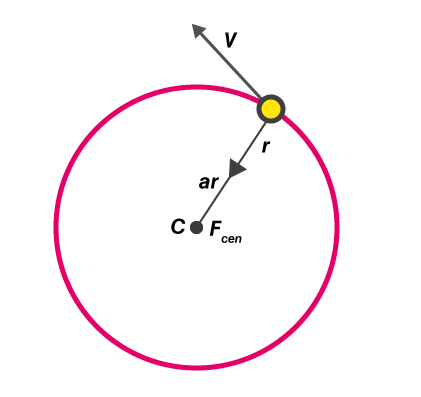
Circular Motion Basics
When an object moves in a circular path at a constant speed, it is still accelerating because the velocity (which includes direction) is constantly changing. This type of acceleration, even without a change in speed, is known as centripetal acceleration. According to Newton's First Law of Motion, an object in motion will continue in a straight line unless acted upon by a resultant force. In circular motion, the resultant force that keeps the object moving in a curved path is the centripetal force, which acts towards the centre of the circle.
Key Terms and Definitions:
- Centripetal Force: The inward force that keeps an object moving in a circle.
- Centripetal Acceleration: The acceleration directed towards the centre of the circular path.
Angular Speed (ω)
Angular speed () represents the angle an object moves through per unit time. It can be calculated using either:
Where:
- = linear speed,
- = radius of the circular path,
- = time period for one full revolution,
- = frequency (number of revolutions per second).
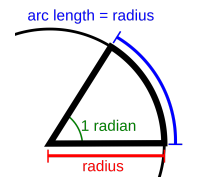
Radians and Angular Measurements
Angles in circular motion are often measured in radians. One radian is the angle formed when the arc length is equal to the radius of the circle. The full circle is radians. Conversions:
- Degrees to radians: multiply by
- Radians to degrees: multiply by
Formulas for Circular Motion
- Centripetal Acceleration ():
This formula shows that acceleration depends on the speed and radius of the circular path.
- Centripetal Force (F): Using Newton's Second Law the formula for centripetal force becomes:
Where:
- = mass of the object,
- = speed of the object,
- = radius of the circle,
- = angular speed.
Example Problem
An object of mass 2 kg is moving at a speed of 5 m/s in a circular path of radius 3 m. Calculate the centripetal force acting on the object.
Solution: Using the centripetal force formula:
Substitute values:
Thus, the centripetal force is 16.67 N.
500K+ Students Use These Powerful Tools to Master Circular motion For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
40 flashcards
Flashcards on Circular motion
Revise key concepts with interactive flashcards.
Try Physics Flashcards4 quizzes
Quizzes on Circular motion
Test your knowledge with fun and engaging quizzes.
Try Physics Quizzes29 questions
Exam questions on Circular motion
Boost your confidence with real exam questions.
Try Physics Questions27 exams created
Exam Builder on Circular motion
Create custom exams across topics for better practice!
Try Physics exam builder56 papers
Past Papers on Circular motion
Practice past papers to reinforce exam experience.
Try Physics Past PapersOther Revision Notes related to Circular motion you should explore
Discover More Revision Notes Related to Circular motion to Deepen Your Understanding and Improve Your Mastery
