9.2.3 Classification by temperature, black-body radiation

Black-Body Radiator

• A black body is an idealised object that perfectly emits and absorbs all wavelengths of radiation.
• Stars can be approximated as black bodies, which allows us to apply laws of black-body radiation to understand star temperature, size, and luminosity.

Stefan's Law

• Stefan's law states that the power output (luminosity, $( P )$ of a black body radiator is directly proportional to its surface area (A) and the fourth power of its absolute temperature (T)**:

$$P = \sigma A T^4$$

• Where:
  • $\sigma$ is the Stefan-Boltzmann constant $( 5.67 \times 10^{-8} \, \text{W m}^{-2} \text{K}^{-4} )$,
  • $A$ is the surface area of the star,
  • $T$ is the absolute temperature in Kelvin.
• This relationship is useful for comparing stars based on their luminosity, temperature, and size.

Wien's Displacement Law

• Wien's law shows that the peak wavelength $(lambda_{\text{max}} )$ of emitted radiation by a black body is inversely proportional to its absolute temperature (T)**:

$$\lambda_{\text{max}} T = 2.9 \times 10^{-3} \, \text{m K}$$

• This means that as temperature increases, the peak wavelength decreases, implying that hotter objects emit shorter wavelengths.
• Wien's law helps estimate the temperature of stars by observing their peak emission wavelength.

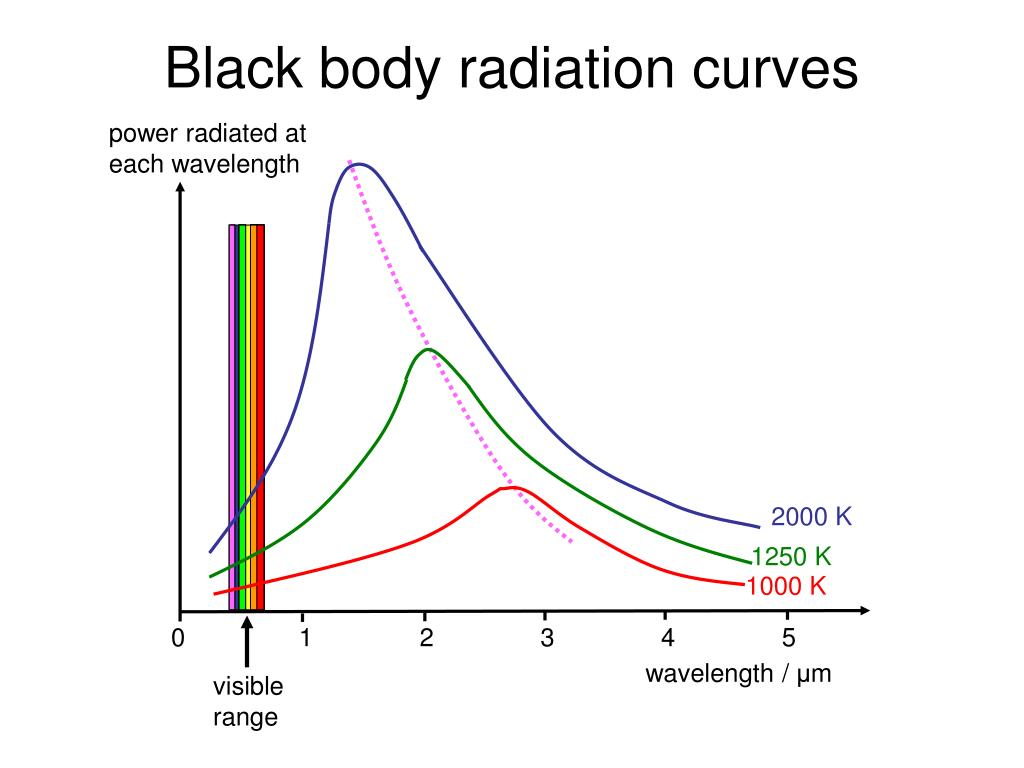
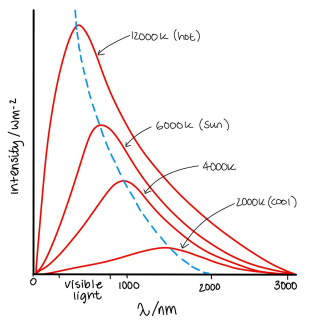
Black-Body Curves

• A black-body curve represents the intensity of radiation emitted by an object against the wavelength of the emitted radiation.
• As the temperature of the black body increases:
  • The peak of the curve shifts to shorter wavelengths (indicating higher energy),
  • The intensity increases, producing a brighter object.
• This principle allows scientists to infer the temperature and other characteristics of stars based on their emission spectrum.

Inverse Square Law of Intensity

• The intensity ($I$) of light emitted by a star decreases with the square of the distance ($d$)** from the star:

$$I = \frac{P}{4 \pi d^2}$$

• Intensity here refers to the power per unit area received from the star.
• This follows the inverse square law because light spreads out equally in all directions from the point source, covering a larger area as the distance increases.