9.2.2 Absolute magnitude

Formula Connecting Apparent and Absolute Magnitude

The relationship between apparent magnitude $m$ and absolute magnitude $M$ can be given by the following formula:

$$m - M = 5 \log \left(\frac{d}{10}\right)$$

Where:

• $d$ is the distance to the star in parsecs ($pc$). This equation allows us to calculate the absolute magnitude if we know the apparent magnitude and distance.

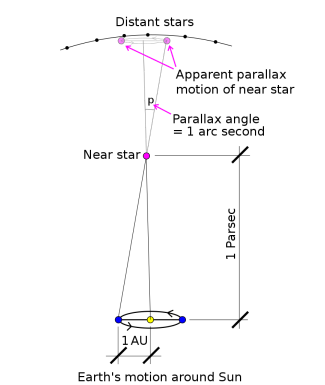
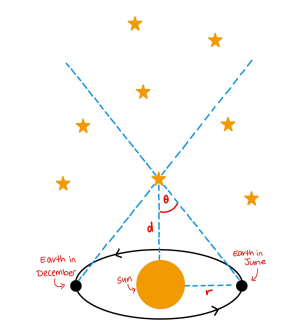
Parallax Method for Distance Measurement

Parallax is the method used to calculate the distance of nearby stars by observing their apparent shift in position against distant stars as Earth orbits the Sun.

• Angle of Parallax $(\theta)$: This is the angle formed by observing the position of a nearby star from opposite sides of Earth's orbit.
• The greater the parallax angle, the closer the star is to Earth.

Units of Distance in Astrophysics

1. Astronomical Unit ($AU$): The average distance between Earth and the Sun, approximately 1.50 × 10¹¹ m.
2. Parsec ($pc$): The distance at which 1 AU subtends an angle of 1 arcsecond ($1/3600th$ of a degree).

• 1 parsec = 3.26 light-years = 3.08 × 10^{16} m.

3. Light-year ($ly$): The distance light travels in one year in a vacuum.

• 1 light-year = 9.46 × 10^{15} m.

Using Parallax to Calculate Distance in Parsecs

To determine the distance of a star using parallax:

4. Use the small angle approximation:

$$\tan \theta \approx \theta \approx \frac{d}{r}$$

Where:

• $d$ is the distance in metres,
• $r$ is $1$ AU, and
• $\theta$ is the parallax angle in radians.

5. This can be simplified to:

$$d = \frac{1}{\theta}$$

where $d$ is in parsecs and $\theta$ is in arcseconds.

Diagrams

Diagrams (such as those shown in the provided content) typically illustrate how parallax works by showing Earth's position at opposite points in its orbit and the resulting apparent shift in the position of a nearby star against a background of distant stars.