Photo AI
Last Updated Sep 27, 2025
Linear Trigonometric Equations Simplified Revision Notes for A-Level OCR Maths Pure
Revision notes with simplified explanations to understand Linear Trigonometric Equations quickly and effectively.
475+ students studying
5.3.2 Linear Trigonometric Equations
Linear trigonometric equations are equations that involve trigonometric functions like sine, cosine, or tangent, and the variable (usually) appears in a linear form, meaning it's not squared, cubed, etc. Solving these equations involves finding all possible angles that satisfy the equation within a given range, often within one full cycle of the trigonometric function (e.g.,) to
1. Basic Steps to Solve Linear Trigonometric Equations:
- Isolate the Trigonometric Function:
- Get the trigonometric function like on one side of the equation.
- Solve for the Angle:
- Use the inverse trigonometric function to find the principal solution. Remember that trigonometric functions are periodic, so there may be multiple solutions within the given interval.
- Consider the General Solution:
- For sine and cosine functions, account for their periodic nature by adding the general solution using (where is an integer) to find all solutions within the specified interval.
- For tangent, since its period is to find all solutions.
- Check the Interval:
- Make sure that the solutions you find are within the given interval (e.g., ).
2. Examples of Solving Linear Trigonometric Equations:
Example 1: Solving = 0.5
- Step 1: Isolate the function:
- Step 2: Find the principal solution: The principal solution is
- Step 3: Consider all solutions: (Because is positive in the first and second quadrants.)
- Step 4: List all solutions within the interval
Example 2: Solving
- Step 1: Isolate the function:
- Step 2: Find the principal solution: The principal solution is
- Step 3: Consider all solutions: (Because is negative in the second and third quadrants.)
- Step 4: List all solutions within the interval
Example 3: Solving
- Step 1: Isolate the function:
- Step 2: Find the principal solution: The principal solution is range, we convert this to
- Step 3: Consider all solutions: (Because is negative in the third and fourth quadrants.)
- Step 4: List all solutions within the interval
Example 4: Solving
- Step 1: Isolate the function:
- Step 2: Find the principal solution: The principal solution is
- Step 3: Consider all solutions: (Because the period of
- Step 4: List all solutions within the interval
3. General Solutions for Trigonometric Equations:
For any trigonometric equation, the general solutions are often given as:
- Sine Equation
- Cosine Equation
- Tangent Equation
Summary:
Linear trigonometric equations involve solving for angles that satisfy trigonometric equations like By isolating the trigonometric function, finding the principal solution, and considering the periodic nature of trigonometric functions, you can find all solutions within a specified interval.
Solving Trig Equations
Example: Solve for
Visual representation of on the graph with solutions indicated.
Solving for
The only think which can penetrate is cos bracket is
Method:
- Cosine both sides:
- Do not YET!!! There are multiple solutions at the moment we use an inverse trig function. Find these.
- Once we have multiple solutions, use them to find x:
Example
Solve for
- Rearrange the equation to solve for :
Extend the interval to accommodate the factor of :
- List out the angles:
- Divide by to find :
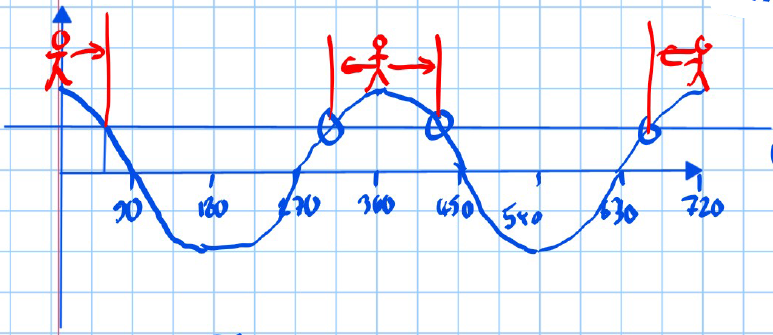
Solve for
- Set up the inequality:
Find the related angle by taking the inverse sine:
- Use the graph to identify additional solutions: Graph shows angles at 135° and 405°.
- Solve for :
Trigonometric Equations
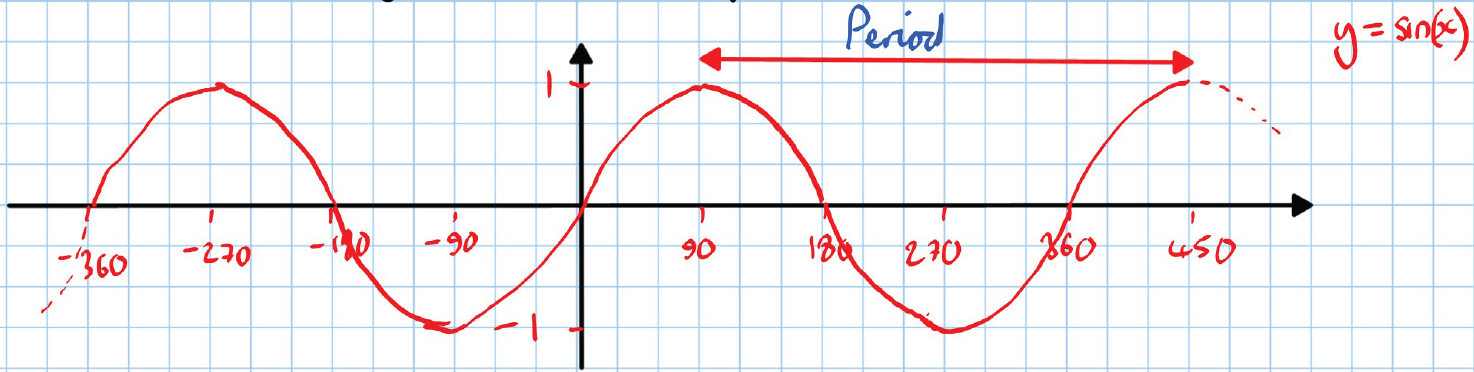
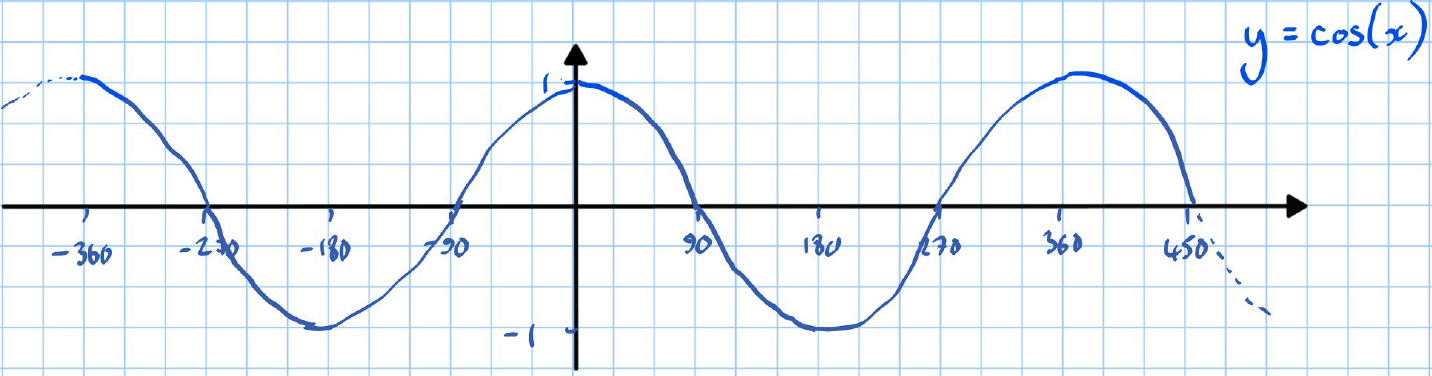
Graphs:
-
- Red graph
-
- Blue graph
-
- Green graph
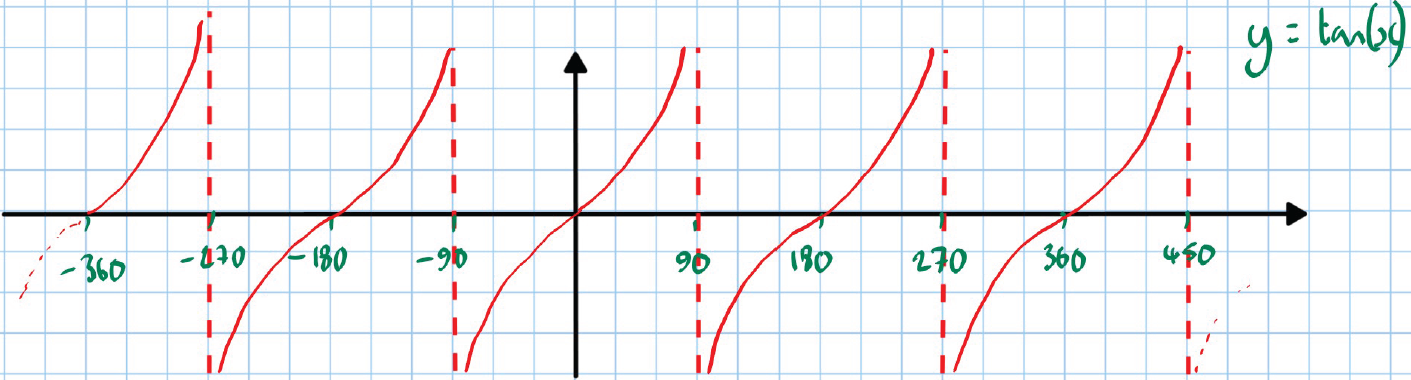
Note: Each graph is labeled with angles in degrees on the x-axis and the function values on the y-axis, showing typical periodic behavior.
Description:
Trigonometric equations, due to the infinite nature of the standard trig functions, typically have an infinite number of solutions. For this reason, in any given equation, we are told the domain in which the solutions are required.
Example:
- Find the first solution on your calculator:
Note: This is not required as a line of working, but it's part of the thought process.
Implied truncation rather than rounding.
- The calculation is done using a calculator, displaying .
Steps to Solve Trigonometric Equations:
-
Sketch the relevant graph within the domain given to identify other solutions.
-
Conclude with all valid solutions:
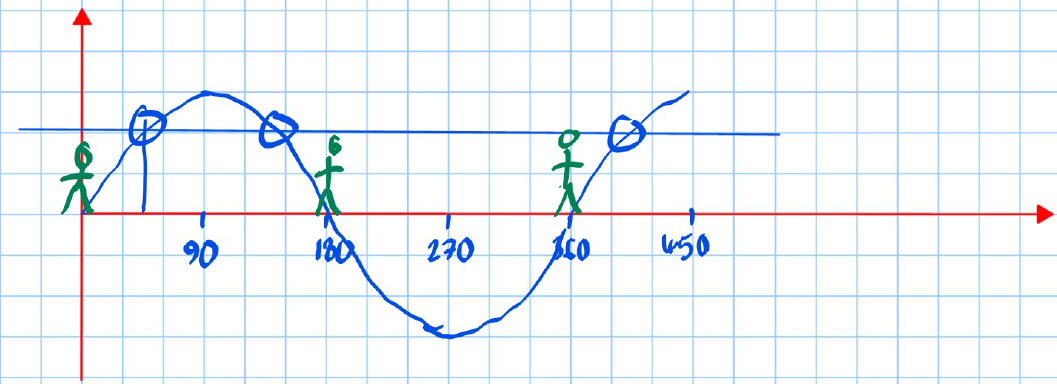
Example:
Solve , for :
-
Initial solution:
-
Note: The initial solution is invalid, but if the graph is extended, it can be used to find valid solutions.
-
Mark the graph and use extensions to find solutions:
-
Solving Trig Equations Involving Compound Angles:
By "compound angle," we mean "an angle more complicated than just ."
- Example: Solve
- Notice we are solving for , but the angle is within the function.
- Method: 3. Modify the domain to find limits for the compound angle in the bracket. 4. Here,
- Solve within the modified domain.
500K+ Students Use These Powerful Tools to Master Linear Trigonometric Equations For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
50 flashcards
Flashcards on Linear Trigonometric Equations
Revise key concepts with interactive flashcards.
Try Maths Pure Flashcards5 quizzes
Quizzes on Linear Trigonometric Equations
Test your knowledge with fun and engaging quizzes.
Try Maths Pure Quizzes29 questions
Exam questions on Linear Trigonometric Equations
Boost your confidence with real exam questions.
Try Maths Pure Questions27 exams created
Exam Builder on Linear Trigonometric Equations
Create custom exams across topics for better practice!
Try Maths Pure exam builder12 papers
Past Papers on Linear Trigonometric Equations
Practice past papers to reinforce exam experience.
Try Maths Pure Past PapersOther Revision Notes related to Linear Trigonometric Equations you should explore
Discover More Revision Notes Related to Linear Trigonometric Equations to Deepen Your Understanding and Improve Your Mastery
96%
114 rated
Trigonometric Equations
Strategy for Trigonometric Equations
485+ studying
199KViews