5.3.1 Trigonometry - Simple Identities

Trigonometric identities are fundamental relationships between trigonometric functions that are true for all values of the variables involved. These identities simplify expressions and solve trigonometric equations. Below are some of the most important and commonly used trigonometric identities.

1. Pythagorean Identities:

These identities are derived from the Pythagorean theorem applied to the unit circle.

infoNote

Basic Pythagorean Identity:

$\sin^2 \theta + \cos^2 \theta = 1$

This identity states that the square of the sine of an angle plus the square of the cosine of the same angle is always equal to $1$ .

Derived Pythagorean Identities:

$1 + \tan^2 \theta = \sec^2 \theta$

This is obtained by dividing the basic Pythagorean identity by $\cos^2 \theta.$

$\csc^2 \theta = 1 + \cot^2 \theta$

This is obtained by dividing the basic Pythagorean identity by $\sin^2 \theta.$

2. Reciprocal Identities:

These identities express the basic trigonometric functions in terms of their reciprocals.

infoNote

Sine and Cosecant:

$\csc \theta = \frac{1}{\sin \theta}$

Cosine and Secant:

$\sec \theta = \frac{1}{\cos \theta}$

Tangent and Cotangent:

$\cot \theta = \frac{1}{\tan \theta}$

3. Quotient Identities:

These identities express tangent and cotangent as the ratio of sine and cosine.

infoNote

Tangent:

$\tan \theta = \frac{\sin \theta}{\cos \theta}$

Cotangent:

$\cot \theta = \frac{\cos \theta}{\sin \theta}$

4. Co-Function Identities:

These identities show the relationship between trigonometric functions of complementary angles.

infoNote

Sine and Cosine:

$\sin(90^\circ - \theta) = \cos \theta$

$\cos(90^\circ - \theta) = \sin \theta$

Tangent and Cotangent:

$\tan(90^\circ - \theta) = \cot \theta$

$\cot(90^\circ - \theta) = \tan \theta$

Secant and Cosecant:

$\sec(90^\circ - \theta) = \csc \theta$

$\csc(90^\circ - \theta) = \sec \theta$

5. Even-Odd Identities:

These identities show how trigonometric functions behave when their angle is negated.

infoNote

Sine and Cosecant (Odd Functions):

$\sin(-\theta) = -\sin \theta$

$\csc(-\theta) = -\csc \theta$

Cosine and Secant (Even Functions):

$\cos(-\theta) = \cos \theta$

$\sec(-\theta) = \sec \theta$

Tangent and Cotangent (Odd Functions):

$\tan(-\theta) = -\tan \theta$

$\cot(-\theta) = -\cot \theta$

6. Sum and Difference Identities:

These identities are used to find the sine, cosine, or tangent of the sum or difference of two angles.

infoNote

Sine of a Sum/Difference:

$\sin(A \pm B) = \sin A \cos B \pm \cos A \sin B$

Cosine of a Sum/Difference:

$\cos(A \pm B) = \cos A \cos B \mp \sin A \sin B$

Tangent of a Sum/Difference:

$\tan(A \pm B) = \frac{\tan A \pm \tan B}{1 \mp \tan A \tan B}$

7. Double Angle Identities:

These identities are used to express trigonometric functions of double angles $2$ $\theta$ .

infoNote

Sine:

$\sin 2\theta = 2 \sin \theta \cos \theta$

Cosine:

$\cos 2\theta = \cos^2 \theta - \sin^2 \theta$

Which can also be written as:

$\cos 2\theta = 2\cos^2 \theta - 1$

$\cos 2\theta = 1 - 2\sin^2 \theta$

Tangent:

$\tan 2\theta = \frac{2\tan \theta}{1 - \tan^2 \theta}$

8. Half-Angle Identities:

These identities are derived from the double angle identities and are used to find the values of trigonometric functions at half an angle.

infoNote

Sine:

$\sin \frac{\theta}{2} = \pm \sqrt{\frac{1 - \cos \theta}{2}}$

Cosine:

$\cos \frac{\theta}{2} = \pm \sqrt{\frac{1 + \cos \theta}{2}}$

Tangent: $\tan \frac{\theta}{2} = \pm \sqrt{\frac{1 - \cos \theta}{1 + \cos \theta}} = \frac{\sin \theta}{1 + \cos \theta} = \frac{1 - \cos \theta}{\sin \theta}$

infoNote

Example Problem Using Identities:

Problem: Prove that $\sec^2 \theta - \tan^2 \theta = 1.$

Solution:

Start with the identity $\sec^2 \theta = 1 + \tan^2 \theta.$
Subtract $\tan^2 \theta$ from both sides:

$\sec^2 \theta - \tan^2 \theta = 1$

Final Answer:

The identity is proved: $\sec^2 \theta - \tan^2 \theta = 1.$

Category	Identity/Form
Pythagorean Identities	$\sin^2 \theta + \cos^2 \theta = 1$
	$1 + \tan^2 \theta = \sec^2 \theta$
	$\csc^2 \theta = 1 + \cot^2 \theta$
Reciprocal Identities	$\csc \theta = \frac{1}{\sin \theta}$
	$\sec \theta = \frac{1}{\cos \theta}$
	$\cot \theta = \frac{1}{\tan \theta}$
Quotient Identities	$\tan \theta = \frac{\sin \theta}{\cos \theta}$
	$\cot \theta = \frac{\cos \theta}{\sin \theta}$
Co-Function Identities	$\sin(90^\circ • \theta) = \cos \theta$
	$\cos(90^\circ • \theta) = \sin \theta$
	$\tan(90^\circ • \theta) = \cot \theta$
	$\cot(90^\circ • \theta) = \tan \theta$
	$\sec(90^\circ • \theta) = \csc \theta$
	$\csc(90^\circ • \theta) = \sec \theta$
Even-Odd Identities	$\sin(-\theta) = -\sin \theta$
	$\cos(-\theta) = \cos \theta$
	$\tan(-\theta) = -\tan \theta$
	$\csc(-\theta) = -\csc \theta$
	$\sec(-\theta) = \sec \theta$
	$\cot(-\theta) = -\cot \theta$
Sum and Difference Identities	$\sin(A \pm B) = \sin A \cos B \pm \cos A \sin B$
	$\cos(A \pm B) = \cos A \cos B \mp \sin A \sin B$
	$\tan(A \pm B) = \frac{\tan A \pm \tan B}{1 \mp \tan A \tan B}$
Double Angle Identities	$\sin 2\theta = 2 \sin \theta \cos \theta$
	$\cos 2\theta = \cos^2 \theta • \sin^2 \theta$
	$\cos 2\theta = 2\cos^2 \theta • 1$
	$\cos 2\theta = 1 • 2\sin^2 \theta$
	$\tan 2\theta = \frac{2\tan \theta}{1 • \tan^2 \theta}$
Half-Angle Identities	$\sin \frac{\theta}{2} = \pm \sqrt{\frac{1 • \cos \theta}{2}}$
	$\cos \frac{\theta}{2} = \pm \sqrt{\frac{1 + \cos \theta}{2}}$
	$\tan \frac{\theta}{2} = \pm \sqrt{\frac{1 • \cos \theta}{1 + \cos \theta}} = \frac{\sin \theta}{1 + \cos \theta} = \frac{1 • \cos \theta}{\sin \theta}$

This table summarises the essential trigonometric identities, making it easier to quickly reference and apply them to various problems.

Summary:

Trigonometric identities simplify complex trigonometric expressions and solve equations. Mastery of these identities, such as Pythagorean, reciprocal, and sum/difference identities, is essential for success in trigonometry and related fields.

Trigonometric Identities

The $\equiv$ Sign:

$\equiv$ means "identical to" and is a stronger statement than =.

infoNote

Examples: 3. $2x = 6$ : In this case, = is appropriate because there are a limited number of values that make the statement true. 4. $5x \equiv 3x + 2x$ : In this case, no matter which value we substitute for $x$ , the statement is true, i.e., $\equiv$ is appropriate.

The key identities to learn are as follows:

$\sin^2 \theta + \cos^2 \theta \equiv$ 1 Learn These
$\frac{\sin \theta}{\cos \theta} \equiv \tan \theta$

Common Misconception:

\sin \theta + \cos \theta \not\equiv 1

Proof of $\sin^2 \theta + \cos^2 \theta \equiv 1$ for Acute Angles

The identity is true for all values of $\theta$ , but this proof only concerns acute angles.

Take a right-angled triangle with hypotenuse 1.

Let $\theta$ be an angle in the triangle.
Label the opposite side $O$ and adjacent side $A$ .

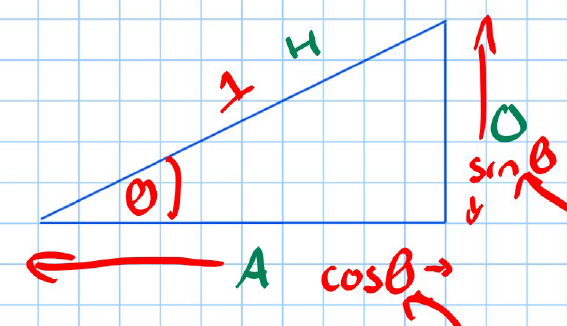
Define Trigonometric Ratios:

$\sin \theta = \frac{\text{Opp}}{\text{Hyp}} \Rightarrow \sin \theta = \text{Opp}\ (\text{since}\ \text{Hypotenuse} = 1)$
$\cos \theta = \frac{\text{Adj}}{\text{Hyp}} \Rightarrow \cos \theta = \text{Adj}\ (\text{since}\ \text{Hypotenuse} = 1)$ From the triangle:
$O = \sin \theta$
$A = \cos \theta$ Thus, by the Pythagorean Theorem:
$O^2 + A^2 = 1 \Rightarrow \sin^2 \theta + \cos^2 \theta = 1$ . $\therefore$ Because the triangle is right-angled,

a^2 + b^2 = c^2

\sin^2\theta + \cos^2\theta \equiv 1

Proof of $\tan\theta = \frac{\sin\theta}{\cos\theta}$ (for acute angles, although true for all angles):

Consider a right triangle with hypotenuse $\text{HYP}$ , opposite side $\text{OPP}$ , and adjacent side $\text{ADJ}$ .

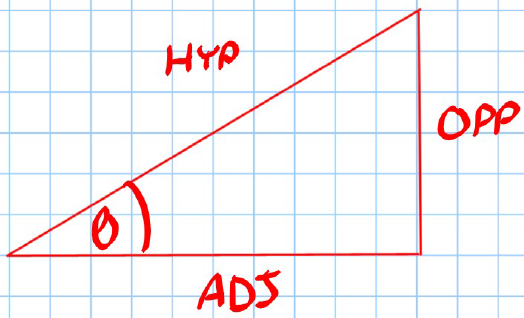
From the triangle:

$\sin\theta = \frac{\text{OPP}}{\text{HYP}}$
$\cos\theta = \frac{\text{ADJ}}{\text{HYP}}$ Thus:

\frac{\sin\theta}{\cos\theta} = \frac{\frac{\text{OPP}}{\text{HYP}}}{\frac{\text{ADJ}}{\text{HYP}}} = \frac {\text{OPP}}{\cancel{\text{HYP}}} \times \frac {\cancel{\text{HYP}}}{\text{ADJ}}=\frac{\text{OPP}}{\text{ADJ}} = \tan\theta

These identities are useful in solving trigonometric equations.

infoNote

Example: Solve: $\quad \cos\theta + 3\sin\theta = 0 \quad \\for \quad0 \leq \theta \leq 360$ .

Thought Process:

Does the question have any square trig functions?
If yes, use

\sin^2\theta + \cos^2\theta \equiv 1.

If no, choose one of:

\sin\theta \equiv \cos\theta \quad \text{or} \quad \frac{\sin\theta}{\cos\theta} \equiv \tan\theta

Following the thought process to the right, it seems sensible to try to manufacture a $\frac{\sin\theta}{\cos\theta}$ .

Steps:

Divide both sides by $\cos\theta$ :

\frac{\cos\theta}{\cos\theta} + 3\frac{\sin\theta}{\cos\theta} = \frac{0}{\cos\theta} \Rightarrow 1 + 3\tan\theta = 0

Solve for $\tan\theta$ :

3\tan\theta = -1 \Rightarrow \tan\theta = -\frac{1}{3}

Use the arctan function:

\theta = \tan^{-1}\left(-\frac{1}{3}\right) \approx -18.435, 161.565, 341.565 \,

Adjust to the correct range $0 \leq \theta \leq 360$ :

\theta \approx 162, 342 \, \, \text{(3 s.f.)}

e.g. $\sin \theta + 2 \cos^2 \theta = -2$

For $-180^\circ \leq \theta \leq 180^\circ$

\Rightarrow \sin \theta + 2(1 - \sin^2 \theta) = -2 \\ \Rightarrow \sin \theta + 2 - 2 \sin^2 \theta = -2 \\ \Rightarrow 2 \sin^2 \theta - \sin \theta - 4 = 0

\Rightarrow \theta = \xcancel{1.686}\quad \text{,} \xcancel{-1.186} \\ \therefore \text{No valid solution}

$2 \cos^2 \theta \Rightarrow$ Since it has $\sin \theta$ & $\cos^2 \theta$ in it, it is recommendable to try to change this using $\sin^2 \theta + \cos^2 \theta \equiv 1$

\sin^2 \theta \equiv 1 - \cos^2 \theta \\ \cos^2 \theta \equiv 1 - \sin^2 \theta

\sin \theta = 3 \sin \theta \cos \theta \hspace{0.5cm} 0 \leq \theta \leq 360

Incorrect Method:

\div \sin \theta \\ \Rightarrow 1 = 3 \cos \theta \\ \Rightarrow \cos \theta = \frac{1}{3}

Because $\sin \theta = 0$ is a solution, we have essentially divided by 0 and 'lost' the solution where $\sin \theta = 0$ .

Correct Method: Factorise

\sin \theta - 3\sin \theta \cos \theta) = 0 \\ \Rightarrow \sin \theta(1-3\cos \theta) = 0 \\ \Rightarrow \sin \theta = 0 \hspace{0.5cm} \text{or} \hspace{0.5cm} 1 - 3 \cos \theta = 0 \\ \Rightarrow \theta = \sin^{-1}(0) = 0

\theta = 0, 180, 360

Beware: The limits at the beginning may be strict inequalities e.g. $0 < x \leq 360$ , invalidating some solutions.

\Rightarrow \theta = 0, 70.5, 180, 289, 360

\Rightarrow 3 \cos \theta = 1 \\ \Rightarrow \cos \theta = \frac{1}{3} \Rightarrow \theta = \cos^{-1} \left(\frac{1}{3}\right) = 70.529

\theta = 70.5, 289^\circ

Show that

5 \sin^2 x + 5 \sin x + 4 \cos^2 x \equiv \sin^2 x + 5 \sin x + 4

5 \sin^2 x + 5 \sin x + 4 \cos^2 x \\ = 5 \sin^2 x + 5 \sin x + 4(1 - \sin^2 x) \\ = 5 \sin^2 x + 5 \sin x + 4 - 4 \sin^2 x \\ = \sin^2 x + 5 \sin x + 4

How do we know what square trig functions to change?

\sin^2 x + 5 \cos^2 x + 2 \cos x = 3

We have a choice of using $\sin^2 x = 1 - \cos^2 x$ or $\cos^2 x = 1 - \sin^2 x$

$2 \cos x$ Cannot change this as it is not squared.

\Rightarrow \text{we are stuck with } \cos x

\therefore 1 - \cos^2 x + 5 \cos^2 x + 2 \cos x = 3 \quad \text{etc...}

Finding One Trig Quantity Given Another

Recap of Identities:

\sin^2 \theta + \cos^2 \theta = 1 \quad \text{or} \quad (\sin \theta)^2 + (\cos \theta)^2 = 1

\tan \theta \equiv \frac{\sin \theta}{\cos \theta}

infoNote

Example: Given that $\sin \theta = \frac{2}{5}$ , find $\cos \theta$ and $\tan \theta$ . In this case, $\theta$ is acute.

Method 1**: Right-Angled Triangle**

Note: This method only works when $\theta$ is acute.

Setup the triangle:
$\sin \theta = \frac{2}{5} = \frac{\text{Opp}}{\text{Hyp}}$
Calculate adjacent:

\text{Adj} = \sqrt{5^2 - 2^2} = \sqrt{21}

Find $\cos \theta$ :

\cos \theta = \frac{\text{ADJ}}{\text{HYP}} = \frac{\sqrt{21}}{5}

Find $\tan \theta$ :

\tan \theta = \frac{\text{OPP}}{\text{ADJ}} = \frac{2}{\sqrt{21}} \times \frac {\sqrt{21}}{\sqrt{21}}= \frac{2 \sqrt{21}}{21}

Method 2: $\sin^2 \theta + \cos^2 \theta = 1$

Note: Works with any angled angle.

\sin \theta = \frac{2}{5}

Use the identity:

\sin^2 \theta + \cos^2 \theta \equiv 1

\left(\frac{2}{5}\right)^2 + \cos^2 \theta \equiv 1

\Rightarrow \frac{4}{25} + \cos^2 \theta \equiv 1 \\\Rightarrow \cos^2 \theta = \frac{21}{25}

\Rightarrow \cos \theta = \pm \frac{\sqrt{21}}{5}

Note**:** $\cos \theta$ is positive since $\theta$ is acute.

Find $\tan \theta$ :

\tan \theta = \frac{\sin \theta}{\cos \theta} = \frac{\frac{2}{5}}{\frac{\sqrt{21}}{5}} = \frac{2 \sqrt{21}}{21}

infoNote

Example: Given that $\theta$ is obtuse, find $\cos \theta$ when $\sin \theta = \frac{1}{2}$ .

$\sin^2 \theta + \cos^2 \theta \equiv 1$

\left(\frac{1}{2}\right)^2 + \cos^2 \theta = 1 \Rightarrow \frac{1}{4} + \cos^2 \theta = 1 \Rightarrow \cos^2 \theta = \frac{3}{4}

\Rightarrow \cos \theta = \pm \frac{\sqrt{3}}{2}

Since $\theta$ is obtuse, $\cos \theta = -\frac{\sqrt{3}}{2}$ .

Given that $\theta$ is reflex and $\cos \theta = \frac{\sqrt{3}}{2}$ , find $\sin \theta$ .

$\sin^2 \theta + \cos^2 \theta \equiv 1$

\sin^2 \theta + \left(\frac{\sqrt{3}}{2}\right)^2 = 1 \Rightarrow \sin^2 \theta = 1 - \frac{3}{4} = \frac{1}{4}

\Rightarrow \sin \theta = \pm \sqrt{\frac{1}{4}} = \pm \frac{1}{2}

Since $\theta$ is reflex, $\sin \theta = -\frac{1}{2}$ .

How to do a good proof

infoNote

Example: (OCR 4722, Q6, June 2010)

Show that $\dfrac{\sin^2 x - \cos^2 x}{1 - \sin^2 x} \equiv \tan^2 x - 1$ .
Hence solve the equation $\dfrac{\sin^2 x - \cos^2 x}{1 - \sin^2 x} = 5 - \tan x, \quad \\ for\ 0^\circ \leq x \leq 360^\circ$ .

Tip: You should always start from the LHS, and your last line should be the RHS.

Part (i):

\text{LHS} = \frac{\sin^2 x - \cos^2 x}{1 - \sin^2 x} = \frac{\sin^2 x - \cos^2 x}{\cos^2 x} = \frac{\sin^2 x}{\cos^2 x} - \frac{\cos^2 x}{\cos^2 x} = \tan^2 x - 1

Note:

\sin^2 x + \cos^2 x \equiv 1 \Rightarrow \frac{\sin^2 x}{\cos^2 x} = \tan^2 x

\frac{\sin^2 x - \cos^2 x}{\cos^2 x} = \tan^2 x - 1

Part (ii):

\tan^2 x - 1 = 5 - \tan x

\tan^2 x + \tan x - 6 = 0

(\tan x - 2)(\tan x + 3) = 0

\tan x = 2 \quad \text{or} \quad \tan x = -3

x = \tan^{-1}(2) \approx 63.435^\circ, 243.435^\circ

x = \tan^{-1}(-3) \approx \xcancel{-71.565^\circ} \Rightarrow 108.435^\circ, 288.435^\circ

Visual representation of solutions on a trigonometric graph.

\therefore x = 63.4^\circ, 108^\circ, 243^\circ, 288^\circ

:::

Proofs Involving Trigonometric Functions

Key Points:

Proofs usually go from left to right (i.e., the right-hand side should be the last thing you write).
Trig proofs do not involve rearranging algebra. We simply use identities to re-present what is already true.

Prove each of the following identities:

a. $\cosec^2 x - \sec^2 x = \cot^2 x - \tan^2 x$

Use Pythagorean identities to re-present the LHS as our target expression.

Notice $\cosec^2 x$ is not part of our target expression, so work at eliminating this from our given expression.

$\sin^2 \theta + \cos^2 \theta \equiv 1$

\xRightarrow{(\div\sin^2\theta)} 1 + \cot^2 \theta \equiv \cosec^2 \theta

LHS = $\cosec^2 x - \sec^2 x$ $= 1 + \cot^2 x - \sec^2 x$

We need this in our answer. Therefore this term is to remain

$\tan^2 \theta + 1 = \sec^2 \theta$

\Rightarrow LHS = \cancel1 + \cot^2 x - (\cancel1 + \tan^2 x) = \cot^2 x - \tan^2 x \quad \text{(proved)}

e. $(\tan x + \cot x)^2 = \sec^2 x + \cosec^2 x$

$\sin^2 \theta + \cos^2 \theta \equiv 1$ $\tan^2 \theta + 1 \equiv \sec^2 \theta$

$\cot^2 \theta + 1 \equiv \cosec^2 \theta$

LHS:

(\tan x + \cot x)^2 = \tan^2 x + 2\tan x \cot x + \cot^2 x

Use identities:

\tan^2 x + 1 = \sec^2 x, \quad \cot^2 x + 1 = \cosec^2 x

Rewrite LHS:

= \tan^2 x + \cot^2 x + 2 \\ \Rightarrow LHS = (\sec^2 x -\cancel{1})+\cancel2+ (\cosec^2 x - \cancel1) \\ \Rightarrow \sec^2 x + \cosec^2 x \quad \text{(proved)}

Note: Only when the Pythagorean formula gives a correct proof should you use $\sec^2 x$ .

$\cosec x = \dfrac{1}{\sin x}, \quad \cot x = \dfrac{\cos x}{\sin x}, \quad \sec x = \dfrac{1}{\cos x}$

h. Prove that $\sec^4 x + \tan^4 x \equiv 2 \sec^2 x \tan^2 x + 1$

\sec^4 x + \tan^4 x = \sec^2 x \sec^2 x + \tan^2 x \tan^2 x

= (\tan^2 x + 1)\sec^2 x + (\sec^2 x - 1)\tan^2 x

= \tan^2 x \sec^2 x + \sec^2 x + \sec^2 x \tan^2 x - \tan^4 x

= 2\tan^2 x \sec^2 x + (\sec^2 x - \tan^2 x) \quad \text{(* using } \tan^2 x - \sec^2 x \equiv 1 \text{)}

= 2\tan^2 x \sec^2 x + 1

Supporting Identities Used

\sin^2 \theta + \cos^2 \theta \equiv 1

\tan^2 \theta + 1 \equiv \sec^2 \theta

\Rightarrow \tan^2 \theta - \sec^2 \theta \equiv 1 \quad (\ast)

Reciprocal Pythagorean Identities

The first Pythagorean identity encountered was $\sin^2\theta + \cos^2\theta = 1$ .

From this, two more identities can be derived:

$\sin^2\theta + \cos^2\theta \equiv 1$ Dividing each side by $\cos^2\theta$ :

\frac {\sin^2\theta}{\cos^2\theta}+\frac {\cos^2\theta}{\cos^2\theta} \equiv \frac {1}{\cos^2\theta}

\tan^2\theta + 1 \equiv \sec^2\theta

$\sin^2\theta + \cos^2\theta \equiv 1$ Dividing each side by $\sin^2\theta$ :

\frac {\sin^2\theta}{\sin^2\theta}+\frac {\cos^2\theta}{\sin^2\theta} \equiv \frac {1}{\sin^2\theta}

1 + \cot^2\theta \equiv \csc^2\theta

infoNote

Example: Solve $\tan^2\theta - 2\sec\theta - 2 = 0 \quad for \quad 0 \leq \theta \leq 2\pi$ .

\tan^2\theta + 1 \equiv \sec^2\theta \Rightarrow \sec^2\theta - 1 = \tan\theta

\sec^2\theta - 1 - 2\sec\theta - 2 = 0

\sec^2\theta - 2\sec\theta - 3 = 0

(\sec\theta - 3)(\sec\theta + 1) = 0

\sec\theta = 3 \quad \text{or} \quad \sec\theta = -1

Reciprocal of both sides

\cos\theta = \frac{1}{3} \quad \text{or} \quad \cos\theta = -1

\theta = \arccos\left(\frac{1}{3}\right) \approx 1.2310, \quad 2\pi - 1.2310

\theta = \arccos(-1) = \pi

\therefore \theta = 1.231, \pi, 5.052

Trigonometry - Simple Identities Simplified Revision Notes for A-Level OCR Maths Pure

5.3.1 Trigonometry - Simple Identities

1. Pythagorean Identities:

2. Reciprocal Identities:

3. Quotient Identities:

4. Co-Function Identities:

5. Even-Odd Identities:

6. Sum and Difference Identities:

7. Double Angle Identities:

8. Half-Angle Identities:

Example Problem Using Identities:

Summary:

Trigonometric Identities

The key identities to learn are as follows:

Common Misconception:

Proof of $\sin^2 \theta + \cos^2 \theta \equiv 1$ for Acute Angles

Proof of $\tan\theta = \frac{\sin\theta}{\cos\theta}$ (for acute angles, although true for all angles):

These identities are useful in solving trigonometric equations.

Finding One Trig Quantity Given Another

Example: Given that $\theta$ is obtuse, find $\cos \theta$ when $\sin \theta = \frac{1}{2}$ .

Given that $\theta$ is reflex and $\cos \theta = \frac{\sqrt{3}}{2}$ , find $\sin \theta$ .

How to do a good proof

Example: (OCR 4722, Q6, June 2010)

Part (i):

Part (ii):

Proofs Involving Trigonometric Functions

Supporting Identities Used

Reciprocal Pythagorean Identities

500K+ Students Use These Powerful Tools to Master Trigonometry - Simple Identities For their A-Level Exams.

Other Revision Notes related to Trigonometry - Simple Identities you should explore

Trigonometry - Simple Identities Simplified Revision Notes for A-Level OCR Maths Pure

5.3.1 Trigonometry - Simple Identities

1. Pythagorean Identities:

2. Reciprocal Identities:

3. Quotient Identities:

4. Co-Function Identities:

5. Even-Odd Identities:

6. Sum and Difference Identities:

7. Double Angle Identities:

8. Half-Angle Identities:

Example Problem Using Identities:

Summary:

Trigonometric Identities

The key identities to learn are as follows:

Common Misconception:

Proof of sin⁡2θ+cos⁡2θ≡1\sin^2 \theta + \cos^2 \theta \equiv 1sin2θ+cos2θ≡1 for Acute Angles

Proof of tan⁡θ=sin⁡θcos⁡θ\tan\theta = \frac{\sin\theta}{\cos\theta}tanθ=cosθsinθ​ (for acute angles, although true for all angles):

These identities are useful in solving trigonometric equations.

Finding One Trig Quantity Given Another

Example: Given that θ\thetaθ is obtuse, find cos⁡θ\cos \thetacosθ when sin⁡θ=12\sin \theta = \frac{1}{2}sinθ=21​.

Given that θ\thetaθ is reflex and cos⁡θ=32\cos \theta = \frac{\sqrt{3}}{2}cosθ=23​​, find sin⁡θ\sin \thetasinθ.

How to do a good proof

Example: (OCR 4722, Q6, June 2010)

Part (i):

Part (ii):

Proofs Involving Trigonometric Functions

Supporting Identities Used

Reciprocal Pythagorean Identities

500K+ Students Use These Powerful Tools to Master Trigonometry - Simple Identities For their A-Level Exams.

Other Revision Notes related to Trigonometry - Simple Identities you should explore

Proof of $\sin^2 \theta + \cos^2 \theta \equiv 1$ for Acute Angles

Proof of $\tan\theta = \frac{\sin\theta}{\cos\theta}$ (for acute angles, although true for all angles):

Example: Given that $\theta$ is obtuse, find $\cos \theta$ when $\sin \theta = \frac{1}{2}$ .

Given that $\theta$ is reflex and $\cos \theta = \frac{\sqrt{3}}{2}$ , find $\sin \theta$ .