Photo AI
Last Updated Sep 27, 2025
Area between 2 curves Simplified Revision Notes for A-Level OCR Maths Pure
Revision notes with simplified explanations to understand Area between 2 curves quickly and effectively.
393+ students studying
8.2.10 Area between 2 curves
Integration: Further Area
Area Between Two Curves
Find the area of the shaded region .
Area between the uppermost curve and the -axis, take the area between the lowermost curve and the -axis.
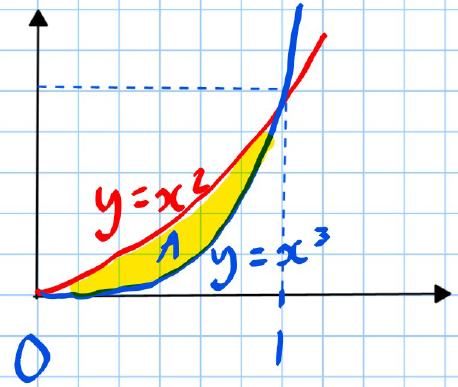
Therefore:
Alternative Method
Area Between a Curve and the -Axis
The formula for the area under a curve (i.e., between the curve and the -axis) is:
The formula for the area between a curve and the -axis is:
Example: Find the shaded area in the following diagram:
- Rearrange the equation to say
- Find the -limits
- Perform the integration
Q1**. (OCR 4722, Jan 2010, Q5)**
The diagram shows parts of the curves and , which intersect at (1, 2) and (3, 10). Use integration to find the exact area of the shaded region enclosed between the two curves.
- Find the area between the "upper curve" (red) and the x-axis:
- Find the area between the "lower curve" (blue) and the -axis:
- Subtract:
Alternative Method: Subtract Before Evaluating Limits
Q2. (OCR 4722, Jan 2012, Q7)
(a) Find .
(b)
The diagram shows the curve and part of the curve , which intersect at the point (1, 6). Use integration to find the area of the shaded region enclosed by the two curves and the x-axis.
Be careful in situations in which the area is not contained from above and below by two curves.
- Region (A)
- Region (B) Root of :
- Total Area:
Integration: Area Between a Curve and the -Axis
To find the area between a curve and the -axis, we calculate:
To find the area between a curve and the -axis, we calculate:
Example:
Find the shaded area for .
- Rearrange the equation to the form :
- Find the y-limits:
- When
- When
- Calculate :
Q1. (OCR 4722, Jun 2008, Q5)
The diagram shows the curve .
The shaded region is bounded by the curve, the -axis, and two lines parallel to the -axis which meet the curve where and .
Question :
(i) Show that the area of the shaded region is given by
(ii) Hence find the exact area of the shaded region.
Solution
(i) Start with the equation of the curve:
Rearrange to solve for :
When
When
Therefore Area
(ii) Calculate the area using the integral:
Substitute the limits and :
500K+ Students Use These Powerful Tools to Master Area between 2 curves For their A-Level Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
120 flashcards
Flashcards on Area between 2 curves
Revise key concepts with interactive flashcards.
Try Maths Pure Flashcards12 quizzes
Quizzes on Area between 2 curves
Test your knowledge with fun and engaging quizzes.
Try Maths Pure Quizzes29 questions
Exam questions on Area between 2 curves
Boost your confidence with real exam questions.
Try Maths Pure Questions27 exams created
Exam Builder on Area between 2 curves
Create custom exams across topics for better practice!
Try Maths Pure exam builder12 papers
Past Papers on Area between 2 curves
Practice past papers to reinforce exam experience.
Try Maths Pure Past PapersOther Revision Notes related to Area between 2 curves you should explore
Discover More Revision Notes Related to Area between 2 curves to Deepen Your Understanding and Improve Your Mastery
96%
114 rated
Further Integration
Integrating Other Functions (Trig, ln & e etc)
231+ studying
200KViews