Practice Problems

Problems:

---

Problem 1

Explanation: Imagine you have two points on a map, and you want to know how far apart they are and where the halfway point is between them. The distance tells you how far apart the points are, and the midpoint tells you where the exact middle is.

---

Problem 2

Explanation: The slope of a line tells us how steep it is, like how a hill slopes up or down. The equation of the line is like a recipe that shows us all the points that the line passes through.

---

Problem 3

Explanation: If you know how steep a line is (the slope) and where it crosses the y$$-axis (the $y$-intercept), you can easily write the equation of the line. This equation tells you everything you need to know about the line.

---

Problem 4

Explanation: When two lines cross each other, the point where they meet is called the intersection. Finding this point helps us understand exactly where the lines overlap on a graph.

---

Solutions:

---

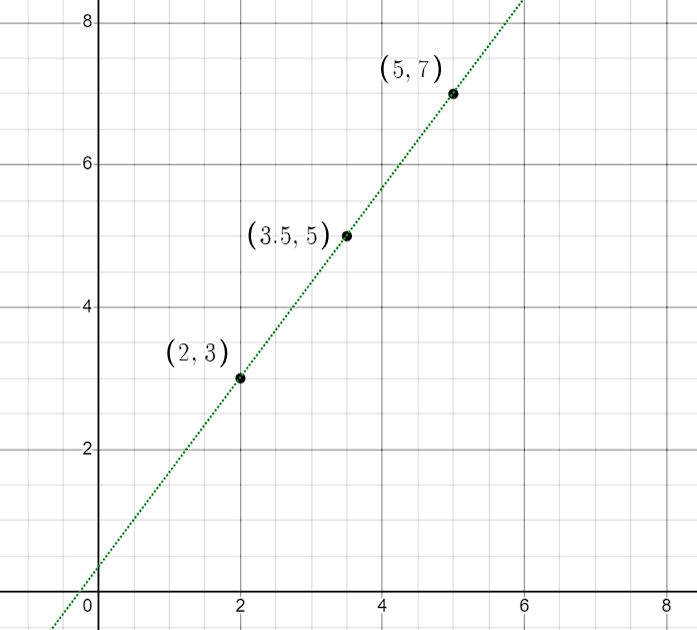
Problem 1

Solution:

We are given two points, $A(2, 3)$ and $B(5, 7)$, and we need to find two things: the distance between them and the midpoint of the line segment that connects them.

Step 1: Find the Distance

To find the distance between two points on a coordinate plane, we use the distance formula:

$\text{Distance } |AB| = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

Here's how to use it step by step:

1. Label the points:

• Point $A$ has coordinates $x_1 = 2$ and $y_1 = 3$.
• Point $B$ has coordinates $x_2 = 5$ and $y_2 = 7$.

2. Substitute the coordinates into the formula: $|AB| = \sqrt{(5 - 2)^2 + (7 - 3)^2}$

3. Simplify the expression:

• Subtract the $x$-coordinates: $5 - 2 = 3$.
• Subtract the $y$-coordinates: $7 - 3 = 4$. $|AB| = \sqrt{3^2 + 4^2}$

4. Square the results:

• $3^2 = 9$
• $4^2 = 16$ $|AB| = \sqrt{9 + 16} = \sqrt{25}$

5. Find the square root: $|AB| = 5$

So, the distance between points $A$ and $B$ is 5 units.

Step 2: Find the Midpoint

To find the midpoint of a line segment, we use the midpoint formula:

$\text{Midpoint} = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right)$

Here's how to use it step by step:

6. Substitute the coordinates into the formula: $\text{Midpoint} = \left(\frac{2 + 5}{2}, \frac{3 + 7}{2}\right)$

7. Add the coordinates and divide by $2$: $\text{Midpoint} = \left(\frac{7}{2}, \frac{10}{2}\right) = \left(3.5, 5\right)$

So, the midpoint of the line segment connecting $A$ and $B$ is (3.5, 5).

---

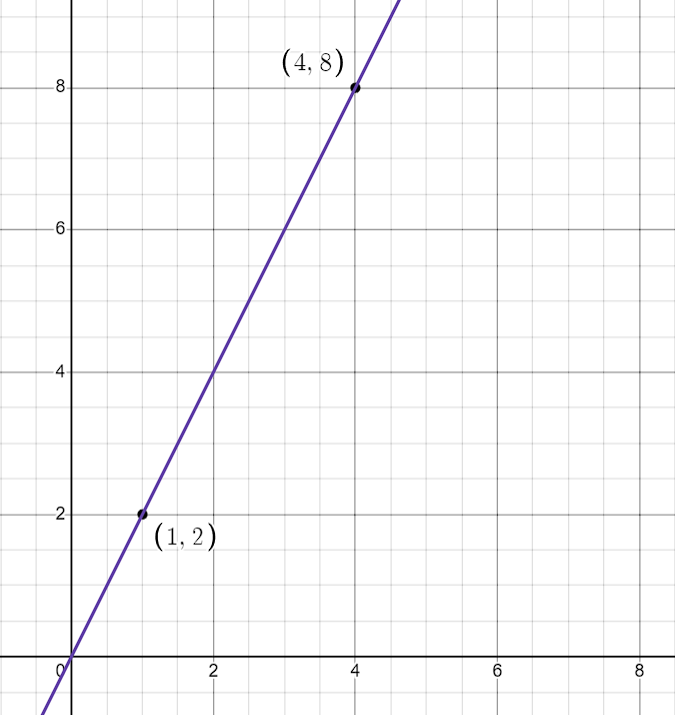
Problem 2

Solution:

We are given two points, $C(1, 2)$ and $D(4, 8)$. We need to find the slope of the line passing through these points and then find the equation of that line.

Step 1: Find the Slope

To find the slope of a line between two points, we use the slope formula:

$\text{Slope } m = \frac{y_2 - y_1}{x_2 - x_1}$

Here's how to use it step by step:

8. Label the points:

• Point $C$ has coordinates $x_1 = 1$ and $y_1 = 2$.
• Point $D$ has coordinates $x_2 = 4$ and $y_2 = 8$.

9. Substitute the coordinates into the formula: $m = \frac{8 - 2}{4 - 1}$

10. Simplify the expression:

• Subtract the y-coordinates: $8 - 2 = 6$.
• Subtract the x-coordinates: $4 - 1 = 3$. $m = \frac{6}{3} = 2$

So, the slope of the line is 2.

Step 2: Find the Equation of the Line

Now that we have the slope $m = 2$, we can use the point-slope formula to find the equation of the line. The point-slope formula is:

$y - y_1 = m(x - x_1)$

Let's use point $C(1, 2)$:

11. Substitute the values: $y - 2 = 2(x - 1)$

12. Expand and simplify:

• Distribute the $2$ on the right-hand side: $y - 2 = 2x - 2$

13. Solve for $y$:

• Add $2$ to both sides: $y = 2x$

So, the equation of the line is y = 2x.

---

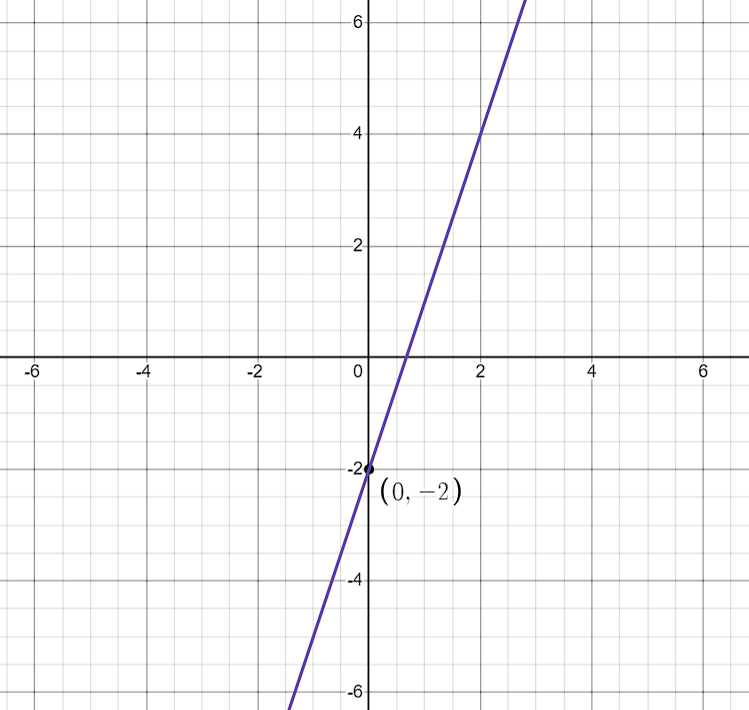
Problem 3

Solution:

We are given that the slope of the line is $m = 3$, and it crosses the $y-axis$ at $y = -2$. This means the y-intercept is$(0, -2)$.

To find the equation of the line, we use the slope-intercept form of a line:

$y = mx + c$

Here's how to use it step by step:

14. Substitute the values:

• The slope $m = 3$.
• The y-intercept $c = -2.$ $y = 3x - 2$

So, the equation of the line is y = 3x - 2.

---

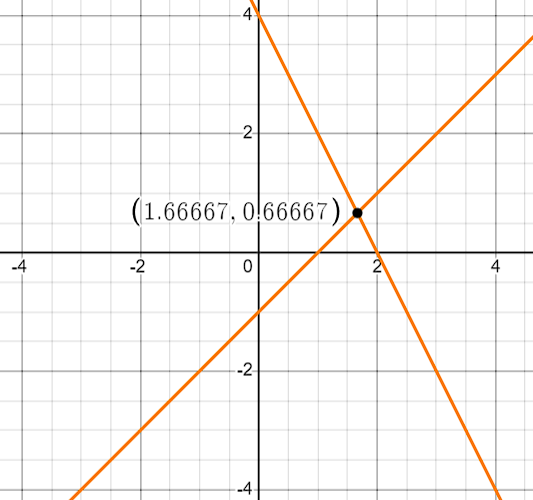
Problem 4

Solution:

We are given two equations:

• $2x + y = 4$ ($Equation A$)
• $x - y = 1$ ($Equation B$) We need to find the point where these two lines intersect by solving the equations simultaneously.

Step 1: Add the Equations to Eliminate $y$

To eliminate $y$, we can add Equation $A$ and Equation $B$. Here's how to do it step by step:

15. Write down the equations:

• Equation A: $2x + y = 4$
• Equation B: $x - y = 1$

16. Add the equations: $(2x + y) + (x - y) = 4 + 1$

Simplify:

$3x = 5$

Step 2: Solve for $x$

Now, solve for $x$ :

$x = \frac{5}{3}$

Step 3: Substitute $x = \frac{5}{3}$ Back into One of the Original Equations

We'll use Equation $B$ to find $y$:

$\frac{5}{3} - y = 1$

Subtract $\frac{5}{3}$ from both sides:

$-y = 1 - \frac{5}{3} = \frac{3}{3} - \frac{5}{3} = \frac{-2}{3}$

Finally, multiply both sides by $-1$:

$y = \frac{2}{3}$

Step 4: Write the Solution as a

Coordinate Pair**

The point of intersection is $\left(\frac{5}{3}, \frac{2}{3}\right)$.

---