Theorems

On the Junior Cycle Maths course, you need to be aware of a number of theorems. These are listed below.

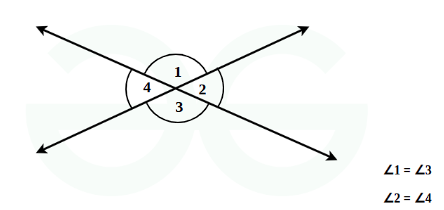
Vertically Opposite Angles Theorem

• What It Says: When two lines cross each other, the angles that are directly across from each other are always equal. So, if you know one of the angles, you automatically know the other one too!

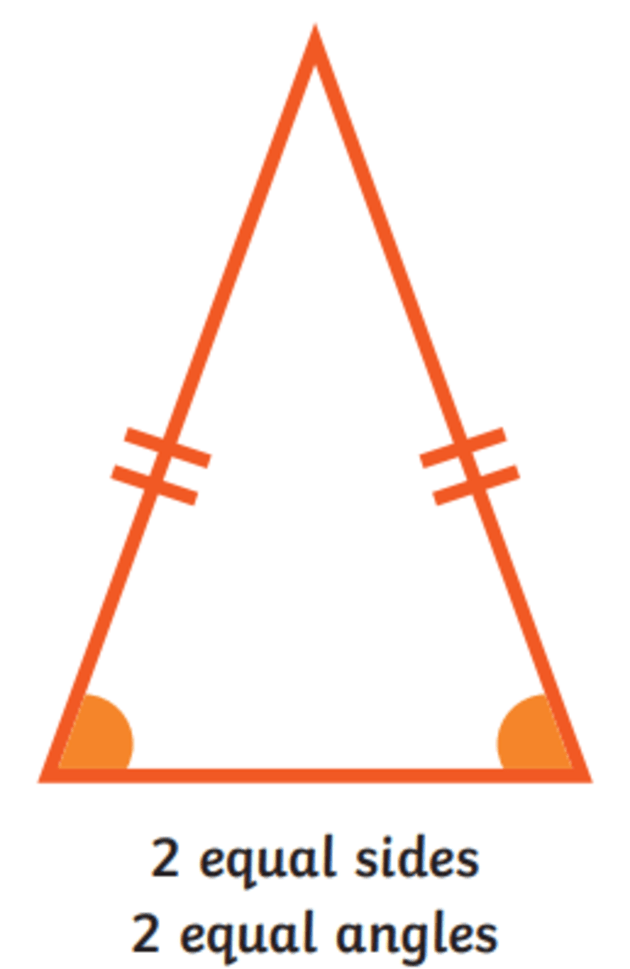
Isosceles Triangle Theorem

• What It Says: In a triangle where two sides are the same length (an isosceles triangle), the angles opposite those sides are also the same. And if you know two angles are equal, you know the sides opposite those angles are equal too.

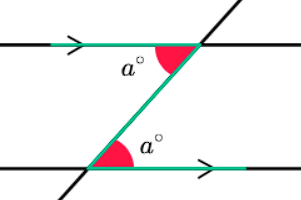
Alternate Angles and Parallel Lines Theorem

• What It Says: If you have two lines that are parallel (they never meet), and another line crosses them, the angles that are on opposite sides of the crossing line (called alternate angles) are equal.

Triangle Angle Sum Theorem

• What It Says: No matter what kind of triangle you have, the three angles inside the triangle will always add up to 180°. This is true for every triangle, big or small.

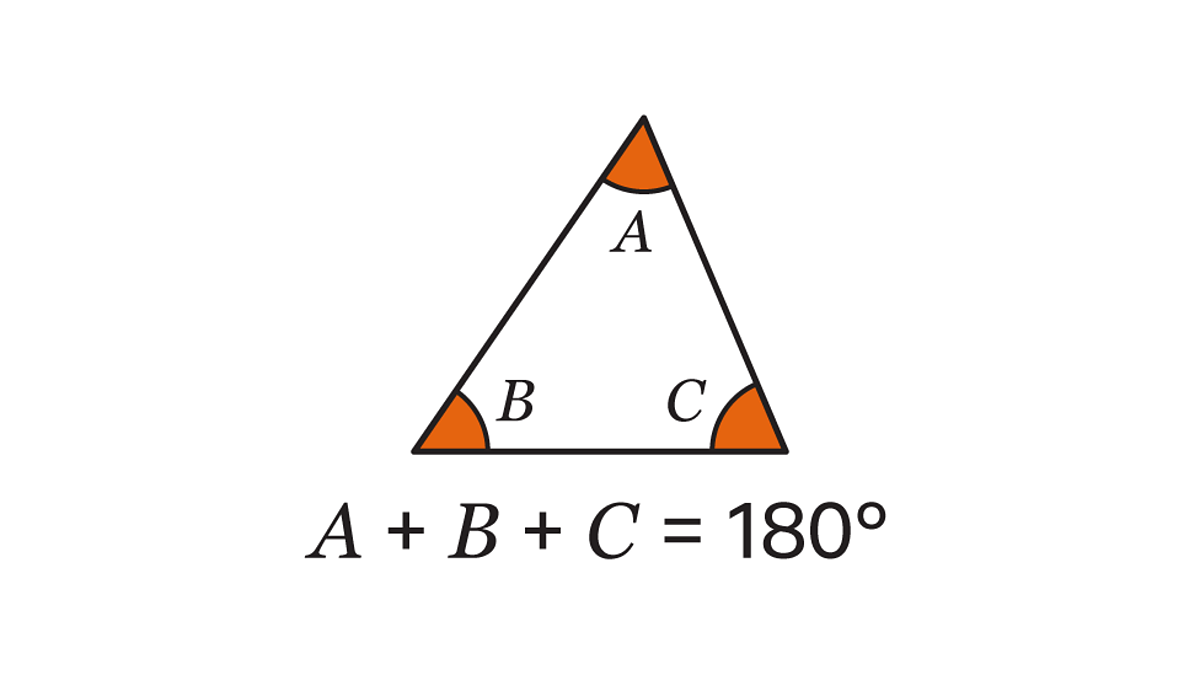
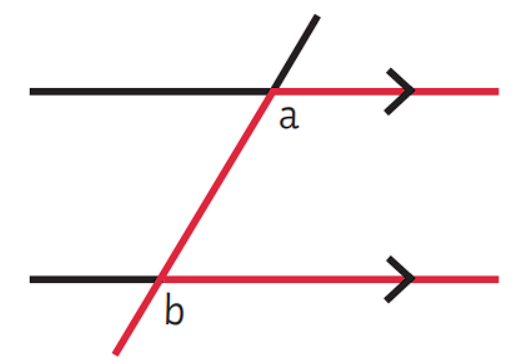
Corresponding Angles and Parallel Lines Theorem

• What It Says: When two lines are parallel and another line crosses them, the angles that are in the same position on each line (called corresponding angles) are equal. If the corresponding angles are equal, then the lines are parallel.

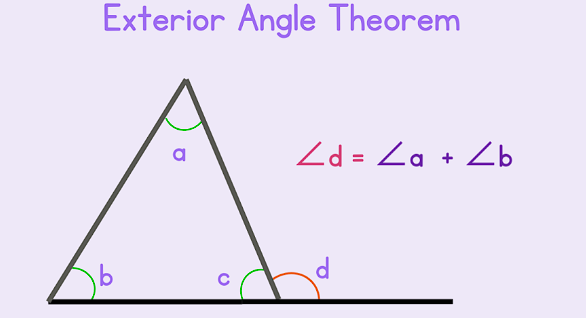
Exterior Angle Theorem

• What It Says: In any triangle, if you extend one side to make an exterior angle, that exterior angle will be equal to the sum of the two opposite angles inside the triangle.

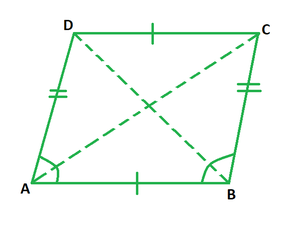
Parallelogram Sides and Angles Theorem

• What It Says: In a parallelogram (a four-sided shape with opposite sides that are parallel), the opposite sides are the same length, and the opposite angles are equal.

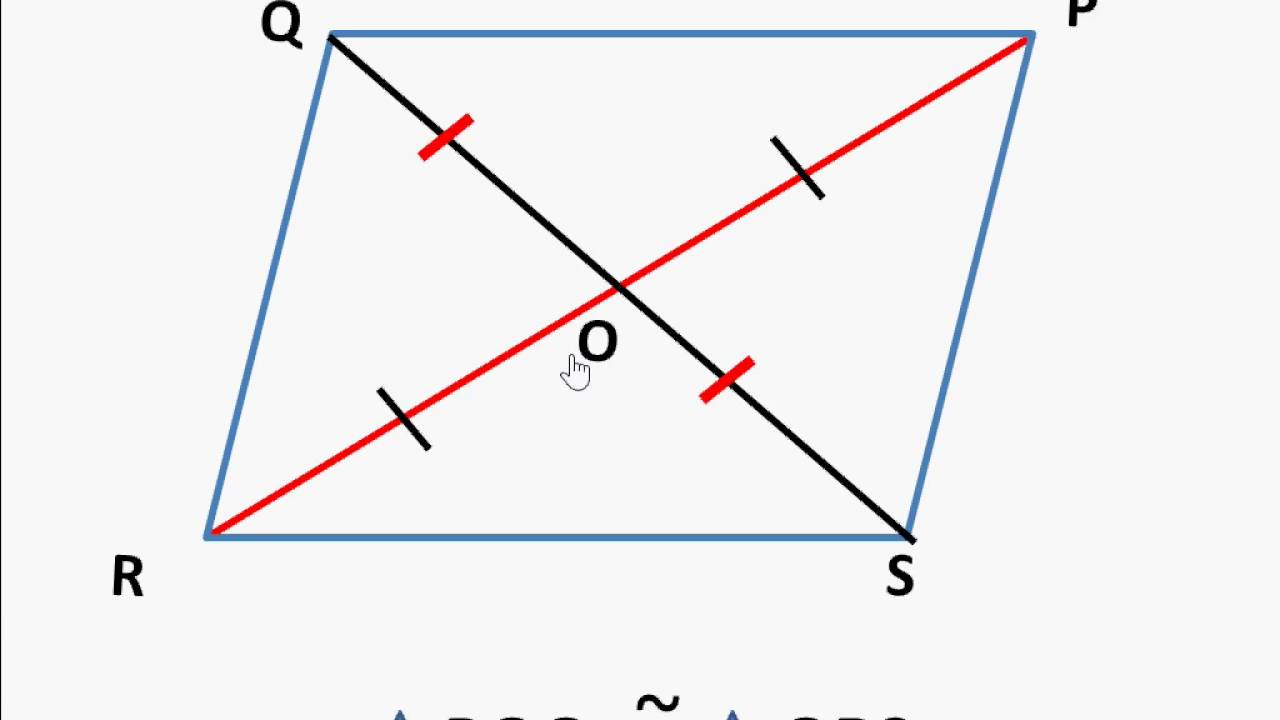
Parallelogram Diagonals Theorem

• What It Says: In a parallelogram, the diagonals (the lines connecting opposite corners) cut each other exactly in half. This means each diagonal divides the other into two equal parts.

Transversal and Parallel Lines Segment Theorem

• What It Says: If you have three parallel lines, and they cut off equal segments on one line that crosses them (a transversal), then they will also cut off equal segments on any other transversal line that crosses them.

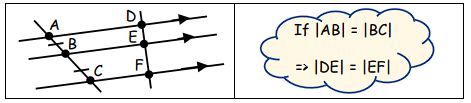
Triangle Proportionality Theorem

• What It Says: If a line is parallel to one side of a triangle and cuts across the other two sides, it divides those sides into equal ratios (proportions). This means the parts of the sides that the line cuts are in the same ratio.

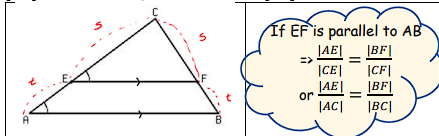
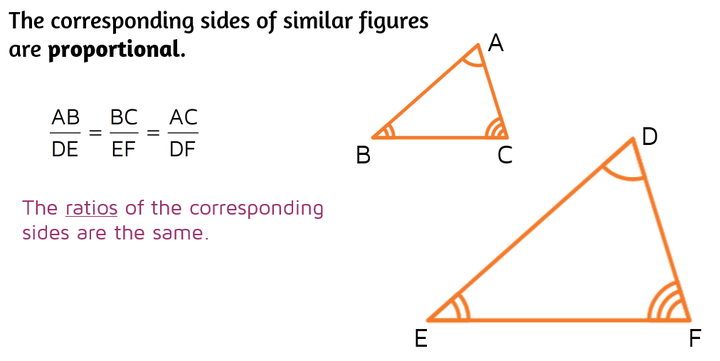
Similar Triangles Theorem

• What It Says: If two triangles have the same shape but not necessarily the same size (they're similar), then their sides are proportional. This means the sides are in the same ratio, even though the triangles might be different sizes.

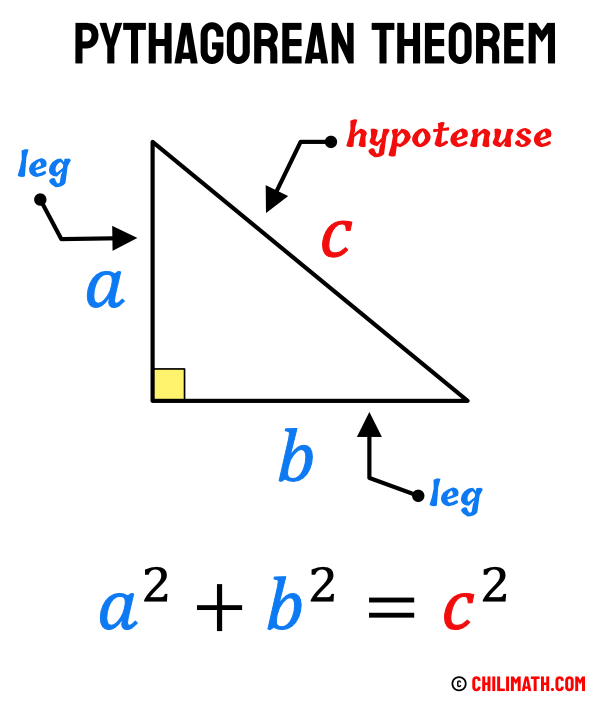
Pythagoras' Theorem

• What It Says: In a right-angled triangle, the square of the longest side (called the hypotenuse) is equal to the sum of the squares of the other two sides. This is a super important theorem for working with right triangles!

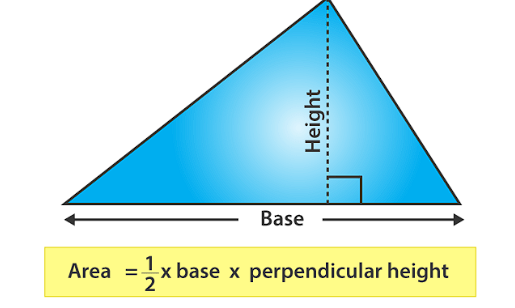
Triangle Area Theorem

• What It Says: The area of any triangle can be found by multiplying the base by the height and then dividing by two. This works no matter which side you choose as the base.

Parallelogram Diagonal Area Theorem

• What It Says: In a parallelogram, a diagonal divides the shape into two equal areas. So if you draw a diagonal, you get two smaller parallelograms that are exactly the same size.

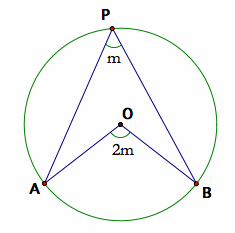
Angle at the Center of a Circle Theorem

• What It Says: The angle at the center of a circle is twice the angle at the edge of the circle, as long as both angles are standing on the same arc. This is a useful fact when working with angles in circles.

---