Photo AI
Last Updated Sep 27, 2025
Max & Min Points (Turning Points) Simplified Revision Notes for Leaving Cert Mathematics
Revision notes with simplified explanations to understand Max & Min Points (Turning Points) quickly and effectively.
366+ students studying
Max & Min Points (Turning Points)
Introduction
For most graphs, you may notice points for which the graph begins to "turn". That is, the graph goes from strictly increasing to strictly decreasing (or vice versa). These points are known as stationary points (or turning points).
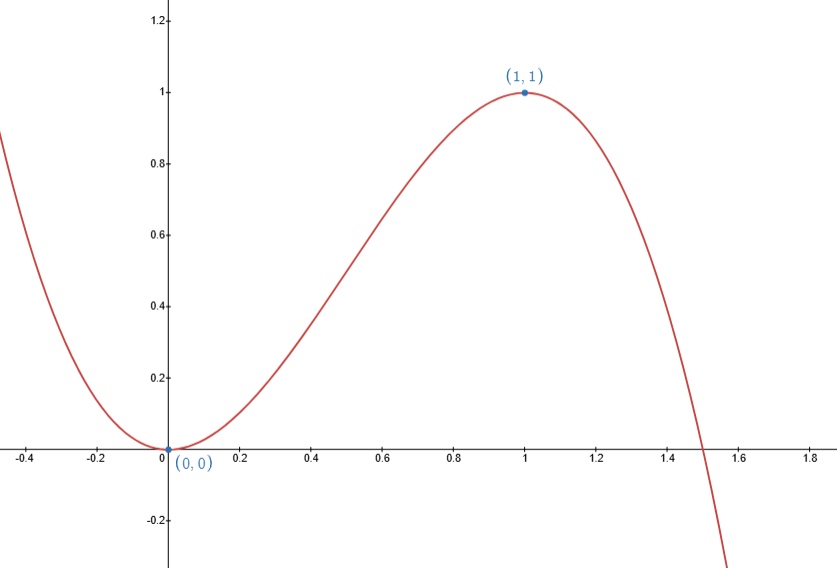
In the following diagram, the turning points are and . At these points exactly, the slope of the tangents is neither increasing nor decreasing. The slope is actually completely flat.
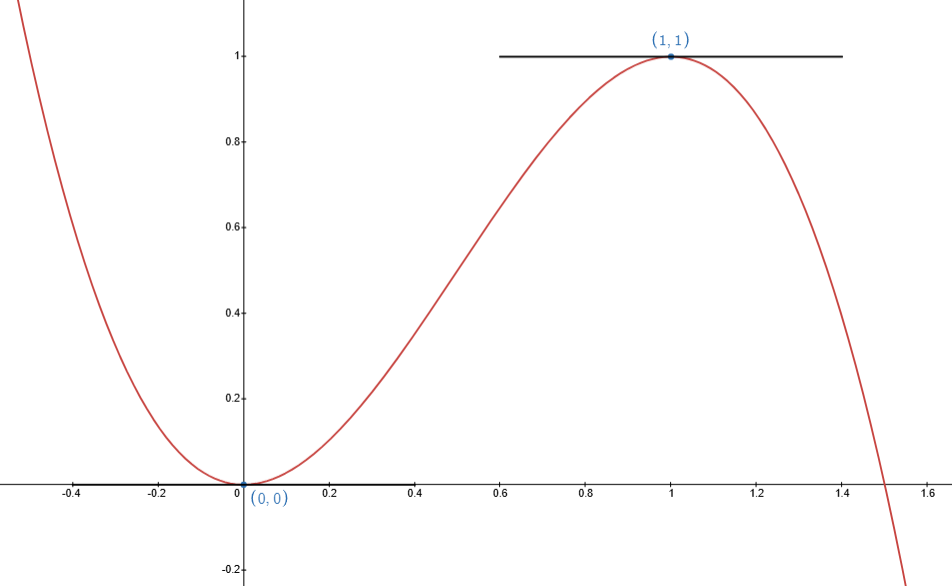
Example
Determine the turning points of the function .
First differentiate the function :
The turning points occur where the slopes of the tangents are flat, so the slope has to be .
We found the coordinates of the turning points, to determine the coordinates, substitute back into the original function.
So, the turning points are :
Second Derivative Test
In the previous example we've determined the turning points of the function, but this doesn't tell us which is the local minima and which one is the local maxima. To find this out, we need to do the second derivative test. Take the second derivative of the function :
If is a turning point, is a local minima if .
If is a turning point, is a local maxima if .
Let's test the point :
, so the point is a local minima.
Now test the point
, so the point is a local maxima.
500K+ Students Use These Powerful Tools to Master Max & Min Points (Turning Points) For their Leaving Cert Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
140 flashcards
Flashcards on Max & Min Points (Turning Points)
Revise key concepts with interactive flashcards.
Try Mathematics Flashcards11 quizzes
Quizzes on Max & Min Points (Turning Points)
Test your knowledge with fun and engaging quizzes.
Try Mathematics Quizzes29 questions
Exam questions on Max & Min Points (Turning Points)
Boost your confidence with real exam questions.
Try Mathematics Questions27 exams created
Exam Builder on Max & Min Points (Turning Points)
Create custom exams across topics for better practice!
Try Mathematics exam builder322 papers
Past Papers on Max & Min Points (Turning Points)
Practice past papers to reinforce exam experience.
Try Mathematics Past PapersOther Revision Notes related to Max & Min Points (Turning Points) you should explore
Discover More Revision Notes Related to Max & Min Points (Turning Points) to Deepen Your Understanding and Improve Your Mastery
