Inverse Functions

The inverse of a function reverses the original function's input-output relationship. If a function $f(x)$ maps $x \to y$, its inverse $f^{-1}(x)$ maps $y \to x$.

Example

Now I can find the original input to any output. For example :

$$f(1)=2(1)+3=5$$ $$f^{-1}(5)=\frac{(5)-3}{2}=1$$

$1$ maps to $5$, $5$ maps back to $1$.

---

A function only has an inverse if it is one-to-one ($1$-to-$1$). For example, $f(x) = x^2, x \in \mathbb{R}$ has no inverse. This function is many-to-one, therefore no inverse exists.

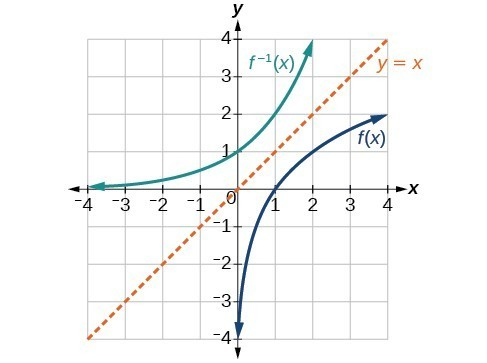
Geometric Relationship between a Function and its Inverse

To find the inverse of a function, we simply swap its $x$ and y values. This is the equivalent of reflecting the graph through the line $y = x$.