Max & Min Problems

We've seen how to derive the local minima and local maxima for a function. This has interesting applications in optimisation problems.

For example, a company produces $x$ cakes. The profit $P(x)$ , in euros, is modelled by the quadratic equation

P(x)=-x^2+10x

Let's graph this out :

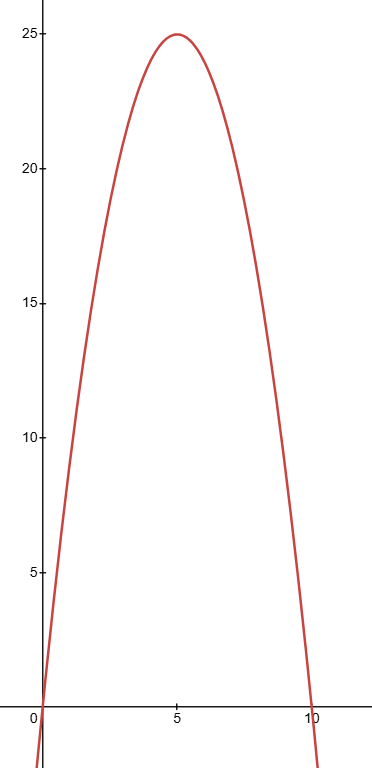
From observation you can see a trade-off.

There's a portion of the graph where the company makes some amount of cakes, but could make more to increase the profit.
There's a portion of the graph where the company makes too much cakes such there profit starts to decrease, maybe because they can't sell the cakes. There is however a single point - the local maximum where the amount of cakes produced yields the highest possible profit.

Simply, derive $P(x)$ :

P'(x)=-2x+10

Now solve for $P'(x)=0$ :

-2x+10=0

x=5

Producing 5 cakes yields the optimal amount of profit.

P(5)=-(5)^2+10(5)=25

25 euro is the optimal profit this company can produce.

Example

infoNote

An rectangular enclosure has a perimeter of 100 metres of fencing. The width of the enclosure is $w$ metres and the length of the enclosure is $l$ metres.

Express $w$ in terms of $l$ .
Find an expression for the area of the enclosure, in terms of $l$
Find the values of $l$ and $w$ that maximise the area of the enclosure.

The perimeter of the enclosure has to equal to 100 metres, which is how much fencing is available.

Hence, the perimeter can be written as :

2l+2w=100

To express $w$ in terms of $l$ , simply isolate $w$ .

2w=100-2l

w=50-l

We know that the area of a rectangle is the length, multiplied by the width.

Area =L \cdot W=l \cdot w

But we need to write this in terms of $l$ (i.e. there shouldn't be a $w$ term in there). In the first portion of the question, we found an expression for $w$ (in terms of $l$ ) which we can substitute in.

\begin{align*} Area &=l \cdot (50-l) \\\\ &= 50l-l^2 \end{align*}

Finally, we need to find the values of $l$ and $w$ that maximise the area of the enclosure. Find the first derivative of the $Area$ function :

Area'=50-2l

Now solve for $Area'=0$ :

50-2l=0

l=25

We know how long $l$ has to be. To find the corresponding $w$ , substitute back into the original expression for $w$ we found.

w=50-l

w=50-(25)

w=25

Example

infoNote

A company needs to manufacture a cylindrical can that holds 1 litre (1000 cm³) of liquid. The cost of the material for the top and bottom is higher than for the side. Find the dimensions that minimize the cost of the material.

Let the radius of the base be $r$ and the height of the cylinder be $h$ . The volume constraint is :

\pi r^2 h =1000

The cost function $C(r)$ involves the surface area: $C = 2\pi r^2$ (for the top and bottom) plus $2\pi r h$ (for the side).

Next, set up the function that needs to be optimised, express $h$ from the volume constraint:

h = \frac{1000}{\pi r^2}

Substitute into the cost function :

C(r) = 2\pi r^2 + 2\pi r \cdot \frac{1000}{\pi r^2} = 2\pi r^2 + \frac{2000}{r}.

Differentiate the function :

C'(r) = 4\pi r - \frac{2000}{r^2}

Find the critical points by setting the derivative be equal to zero :

4\pi r - \frac{2000}{r^2} = 0

4\pi r^3 = 2000

r^3 = \frac{2000}{4\pi} = \frac{500}{\pi} \quad \Rightarrow \quad r = \left(\frac{500}{\pi}\right)^{\frac{1}{3}}

Classify the critical points, i.e. use the second derivative test.

C''(r) = 4\pi + \frac{4000}{r^3}.

Since $C''(r) > 0$ , the cost function $C(r)$ has a local minimum at this critical point.

The optimal radius is :

r = \left(\frac{500}{\pi}\right)^{\frac{1}{3}}.

The optimal height is :

h = \frac{1000}{\pi r^2}.

Max & Min Problems Simplified Revision Notes for Leaving Cert Mathematics

Max & Min Problems

A company needs to manufacture a cylindrical can that holds 1 litre (1000 cm³) of liquid. The cost of the material for the top and bottom is higher than for the side. Find the dimensions that minimize the cost of the material.

500K+ Students Use These Powerful Tools to Master Max & Min Problems For their Leaving Cert Exams.

Other Revision Notes related to Max & Min Problems you should explore