Photo AI
Last Updated Sep 27, 2025
Sine, Cosine, Tan Ratios Simplified Revision Notes for Leaving Cert Mathematics
Revision notes with simplified explanations to understand Sine, Cosine, Tan Ratios quickly and effectively.
321+ students studying
Sine, Cosine, Tan Ratios
Understanding Sin, Cos, and Tan
The Crucial Point about Sin, Cos, and Tan
Right-Angled Triangles Only: Just like Pythagoras' Theorem, all the work involving Sin, Cos, and Tan only applies to right-angled triangles. This is crucial to remember because if the triangle isn't right-angled, these trigonometric ratios won't work directly. You might need to create a right-angled triangle by adding an auxiliary line.
Checking Your Calculator is in the Correct Mode
- Calculator Mode: Before you begin solving problems involving Sin, Cos, and Tan, ensure your calculator is set to the correct mode. If your calculator is in the wrong mode, it might give you incorrect answers even if you're following all the steps correctly.
- How to Check:
- Enter
sin 30into your calculator. - If your calculator shows
0.5, it's in the correct mode (degrees mode). - If not, you need to switch to degrees mode (
DEG).
- Enter
- Switching Modes: On most calculators, you can change the mode by pressing the
MODEbutton and selecting the degrees option (DEG). The exact process may vary slightly depending on your calculator model.
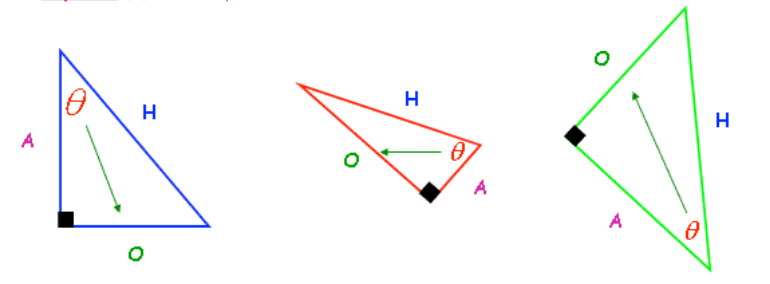
Labelling the Sides of a Right-Angled Triangle
Before you start working out which trigonometric ratio (Sin, Cos, or Tan) you need, it's essential to correctly label the sides of your right-angled triangle.
-
Steps to Label the Sides:
- Hypotenuse (): This is the longest side, always opposite the right angle.
- Opposite (): This is the side directly opposite the angle (the angle you are given or need to find).
- Adjacent (): This is the remaining side, the one next to the angle but not the hypotenuse.
-
Remember: The angle (theta) is often used to represent an unknown angle in mathematics, just as is commonly used for unknown lengths.
Two Ways of Solving Trigonometry Problems
When tackling trigonometry problems in GCSE Maths, you have two main methods to choose from. Both methods are equally valid, so it's up to you to decide which one you prefer.
Steps Before Solving:
- Label
- Tick
- Tick
- Decide
- Label your right-angled triangle.
- Tick the information you know (lengths of sides, sizes of angles).
- Tick the information you need to work out.
- Decide whether the question requires using Sin, Cos, or Tan.
Method A: Use the Formula and Re-arrange
This method is best for students who are comfortable and confident with re-arranging formulas.
- Key Formulas:
- Steps: 4. Substitute the two known values into the appropriate formula. 5. Re-arrange the equation to solve for the unknown value.
Method B: Use the Formula Triangles
This is a clever way of solving trigonometry problems without needing to re-arrange formulas. Instead, you rely on a visual aid—the formula triangle.
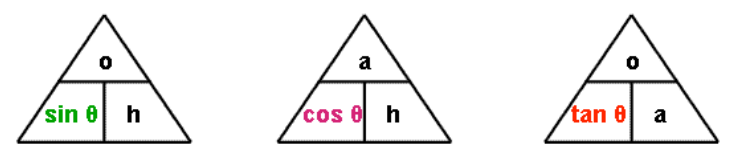
- Formula Triangles:
- For Sin:
- Cover the side you are solving for and use the remaining part of the triangle.
For example:
- For Cos:
Example:
- For Tan:
Example:
- Memory Aid:
- SOHCAHTOA:
- SOH: Sin = Opposite / Hypotenuse
- CAH: Cos = Adjacent / Hypotenuse
- TOA: Tan = Opposite / Adjacent
Example: Solving a Trigonometry Problem Using Tan
Let's work through an example step by step to see how we can use the tangent (Tan) function to solve a trigonometry problem involving a right-angled triangle.
Problem: Find the length of the opposite side in the right-angled triangle where the angle is and the adjacent side is .
Step-by-Step Solution:
- Label the sides:
-
Hypotenuse (): The longest side, opposite the right angle.
-
Opposite (): The side opposite the angle you are working with.
-
Adjacent (): The side next to the angle, but not the hypotenuse. In this triangle:
-
The side we need to find is the Opposite ().
-
We know the Adjacent side () is .
-
The angle θis .
- Identify what you are given:
- We are given the angle and the length of the adjacent side.
- Identify what you need to find:
- We need to find the length of the opposite side ().
- Choose the correct trigonometric ratio:
- Since we know the adjacent side and need to find the opposite side, we use the Tan function because:
- Set up the equation:
- Use the formula:
Substituting the known values:
- Solve for the unknown:
- Rearrange the equation to solve for :
- Use your calculator to find .
- Multiply:
- Final answer:
- The length of the opposite side is approximately (to decimal place).
Example: Solving a Trigonometry Problem Using Cosine (Cos)
Let's go through a problem that requires the use of the cosine (Cos) function to find the length of the hypotenuse in a right-angled triangle.
Problem: Find the length of the hypotenuse in a right-angled triangle where the angle is and the adjacent side is m.
Step-by-Step Solution:
- Label the sides:
-
Hypotenuse (): The longest side, opposite the right angle.
-
Opposite (): The side opposite the angle .
-
Adjacent (A): The side next to the angle , but not the hypotenuse. In this triangle:
-
The side we need to find is the Hypotenuse ().
-
We know the Adjacent side () is 3.1$$m.
-
The angle is .
- Identify what you are given:
- We are given the angle and the length of the adjacent side.
- Identify what you need to find:
- We need to find the length of the hypotenuse ().
- Choose the correct trigonometric ratio:
- Since we know the adjacent side and need to find the hypotenuse, we use the Cosine (Cos) function because:
- Set up the equation:
- Use the formula:
Substituting the known values:
- Solve for the unknown:
- Rearrange the equation to solve for :
- Use your calculator to find cos$$(26\degree)≈0.8988.
- Calculate:
- Final answer:
- The length of the hypotenuse is approximately (to decimal places).
Example: Finding the Angle Using Sine (Sin)
In this example, we will use the Sine function to determine the angle in a right-angled triangle.
Problem: Find the angle in a right-angled triangle where the opposite side to the angle is mm, and the hypotenuse is mm.
Step-by-Step Solution:
- Label the sides:
-
Hypotenuse (): The longest side, opposite the right angle.
-
Opposite (): The side directly opposite the angle .
-
Adjacent (): The side next to the angle , but not the hypotenuse. In this triangle:
-
The Hypotenuse () is .
-
The Opposite side () is .
-
We need to find the angle .
- Identify what you are given:
- We are given the lengths of the opposite side and the hypotenuse.
- Identify what you need to find:
- We need to find the angle .
- Choose the correct trigonometric ratio:
- Since we know the opposite side and the hypotenuse, we use the Sine (Sin) function because:
- Set up the equation:
- Use the formula:
Substituting the known values:
- Calculate the sine of the angle:
- Calculate:
- Find the angle :
- To find , you need to use the inverse sine function :
- Using a calculator:
- Final answer:
- The angle is approximately (to decimal places).
Example: Finding the Length of the Base in an Isosceles Triangle
In this example, we will use the Tangent (Tan) function to determine the length of the base of an isosceles triangle.
Problem: Find the base of the isosceles triangle with two equal sides of cm and the angle between them being .
Step-by-Step Solution:
- Label the sides:
-
Hypotenuse (): The longest side, opposite the right angle.
-
Opposite (): The side directly opposite the angle we are dealing with.
-
Adjacent (): The side next to the angle but not the hypotenuse. For this problem:
-
The Hypotenuse () is (one of the equal sides).
-
The Opposite side () is the height of the triangle (we will find this as an intermediate step).
-
The Adjacent side () is half of the base (we will find this).
- Identify what you are given:
- The Hypotenuse () is .
- The angle is .
- Identify what you need to find:
- The length of the base, which is twice the length of the adjacent side () of the right-angled triangle we can create.
- Use trigonometry to solve:
- Since we have the angle and the opposite side, and we need to find the adjacent side, we use the Tangent (Tan) function:
Rearranging the formula to solve for :
Substituting the values:
- Calculate:
- Using a calculator:
- Double the Adjacent to get the full base:
- Since we only calculated half the base (), double it to find the full length:
- Final answer:
- The full length of the base of the isosceles triangle is approximately .
500K+ Students Use These Powerful Tools to Master Sine, Cosine, Tan Ratios For their Leaving Cert Exams.
Enhance your understanding with flashcards, quizzes, and exams—designed to help you grasp key concepts, reinforce learning, and master any topic with confidence!
100 flashcards
Flashcards on Sine, Cosine, Tan Ratios
Revise key concepts with interactive flashcards.
Try Mathematics Flashcards4 quizzes
Quizzes on Sine, Cosine, Tan Ratios
Test your knowledge with fun and engaging quizzes.
Try Mathematics Quizzes29 questions
Exam questions on Sine, Cosine, Tan Ratios
Boost your confidence with real exam questions.
Try Mathematics Questions27 exams created
Exam Builder on Sine, Cosine, Tan Ratios
Create custom exams across topics for better practice!
Try Mathematics exam builder322 papers
Past Papers on Sine, Cosine, Tan Ratios
Practice past papers to reinforce exam experience.
Try Mathematics Past PapersOther Revision Notes related to Sine, Cosine, Tan Ratios you should explore
Discover More Revision Notes Related to Sine, Cosine, Tan Ratios to Deepen Your Understanding and Improve Your Mastery
