The Unit Circle

Overview

The unit circle is a circle with a radius of $1$ unit, centred at the origin $(0, 0)$ on the coordinate plane. It is a foundational tool in trigonometry, connecting angles to their sine, cosine, and tangent values. The unit circle helps visualize these trigonometric functions and understand their periodic nature.

---

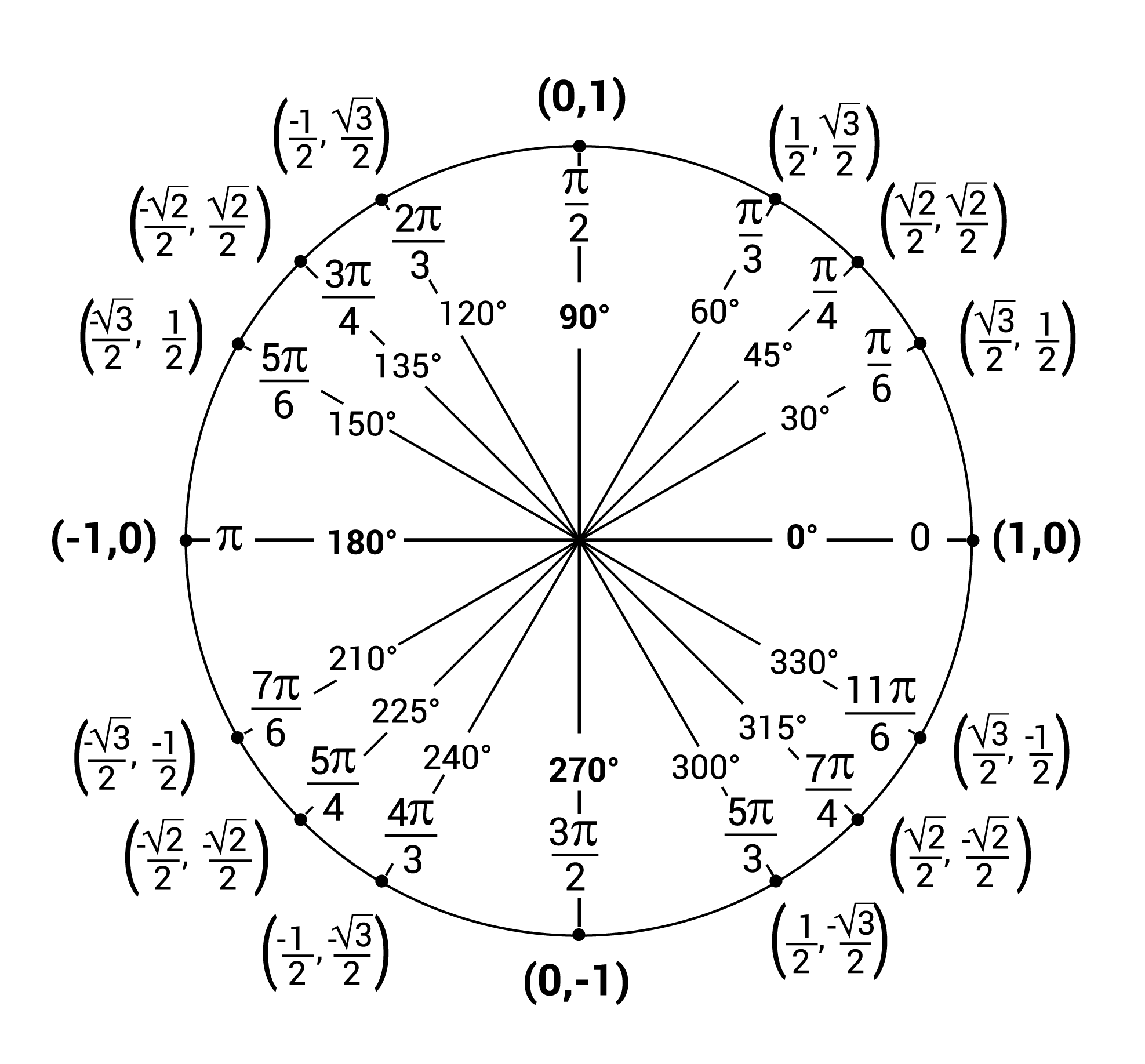
Key Features of the Unit Circle

Coordinates Represent Sine and Cosine

• Any point on the unit circle can be represented as $(\cos \theta, \sin \theta)$, where $\theta$ is the angle formed with the positive $x$-axis.
• The $x$-coordinate gives $\cos \theta$, and the y-coordinate gives $\sin \theta$

Angles in Radians and Degrees

Angles can be measured in degrees or radians:

$$0^\circ = 0 \, \text{radians}$$ $$90^\circ = \frac{\pi}{2}$$ $$180^\circ = \pi$$ $$270^\circ = \frac{3\pi}{2}$$ $$360^\circ = 2\pi$$

Angles are positive when measured counterclockwise and negative when measured clockwise.

Key Quadrants

Quadrant I:

$$0^\circ \leq \theta \leq 90^\circ$$

($\sin \theta$ and $\cos \theta$ are positive).

Quadrant II:

$$90^\circ \leq \theta \leq 180^\circ$$ $$(:highlight[\sin \theta > 0], :highlight[\cos \theta < 0])$$

Quadrant III:

$$180^\circ \leq \theta \leq 270^\circ$$

($\sin \theta$ and $\cos \theta$ are negative).

Quadrant IV:

$$270^\circ \leq \theta \leq 360^\circ$$ $$:highlight[\sin \theta < 0], :highlight[\cos \theta > 0]$$

Key Points on the Unit Circle

• $(1, 0)$ at $0^\circ$ or $360^\circ$
• $(0, 1)$ at $90^\circ$ or $\frac{\pi}{2}$
• $(-1, 0)$ at $180^\circ$ or $\pi$
• $(0, -1)$ at $270^\circ$ or $\frac{3\pi}{2}$

---

Applications

Finding Trigonometric Ratios

Use the unit circle to find values of $\sin \theta$, $\cos \theta$, and $\tan \theta$ for common angles.

Symmetry in Trigonometric Functions

The unit circle reveals symmetry:

• $\sin(-\theta) = -\sin(\theta)$
• $\cos(-\theta) = \cos(\theta)$
• $\tan(-\theta) = -\tan(\theta)$

---

Worked Examples

---

---

Summary

• Unit Circle: A circle with radius $1$ centered at the origin.
• Key Concept: Coordinates represent $(\cos \theta, \sin \theta)$
• Applications: Simplifies trigonometric calculations and reveals symmetry.
• Key Angles and Quadrants: Helps in determining signs and values of trigonometric functions. The unit circle is a crucial tool for mastering trigonometry and understanding the behaviour of trigonometric functions.