Definition

Introduction

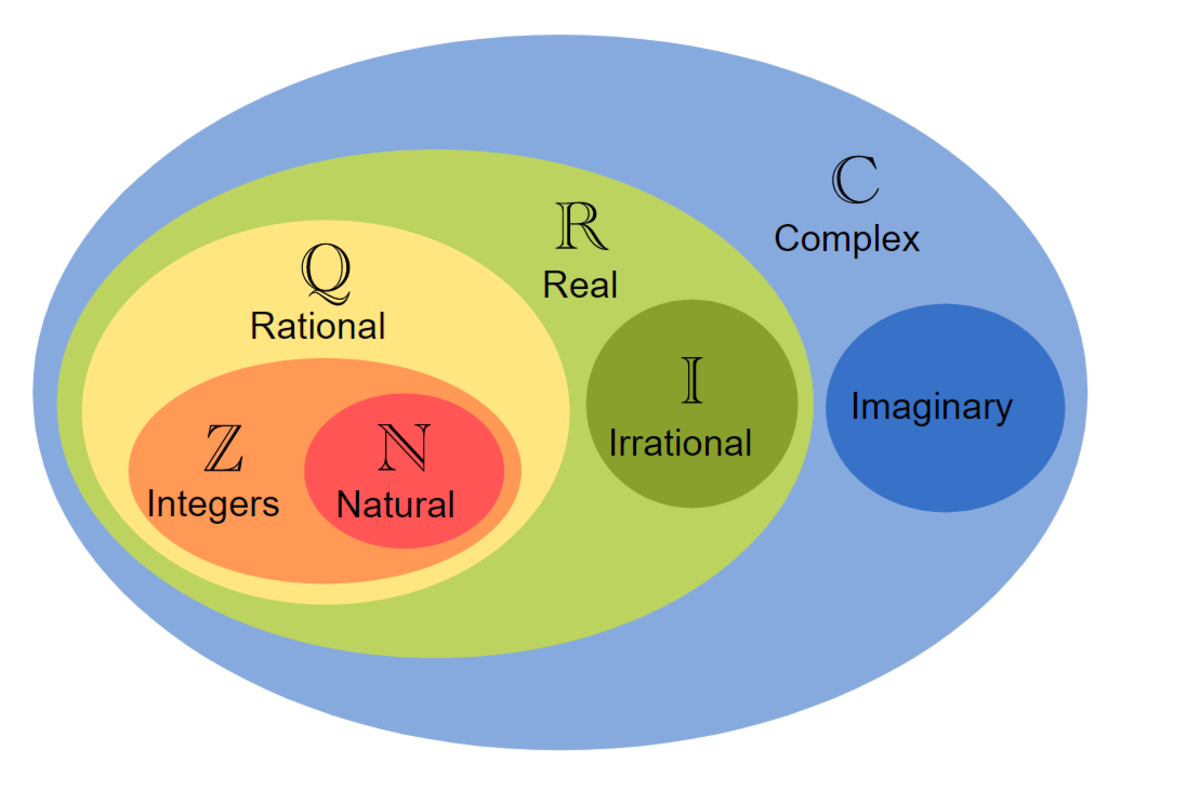
Imaginary numbers are an extension of the real number system and are the foundation of the field of complex numbers. They arise from the need to solve certain equations, particularly those involving square roots of negative numbers, which have no solutions in the real numbers.

Consider the equation : $x^2=-1$. No such solution exists in the real numbers i.e. you need two identical numbers such that their product is $-1$. Euler, assumed that there is such as solution, and gave it the name $i$.

---

Example

Example

Powers of an Imaginary Number

Let's take incremental powers of an imaginary number and see what happens :

• $i^1=i$
• $i^2=\sqrt{-1} \cdot \sqrt{-1}=-1$
• $i^3=i \cdot i^2=\sqrt{-1} \cdot -1=-i$
• $i^4=i^2 \cdot i^2=-1\cdot -1=1$
• $i^5=i^3 \cdot i^2=-i\cdot -1=i$
• $i^6=i^3 \cdot i^3=-i\cdot -i=i^2=-1$
• $i^7=i^4 \cdot i^3=1\cdot -i=-i$ If we keep taking incremental powers we end up with the sequence $i,-1,-i,1$ which repeats. This is very useful as it allows us to quickly derive high powers of $i$.

Example